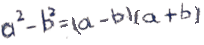Скрыть меню

Особенно нравилась математика верностью и очевидностью своих рассуждений.Рене Декарт

Для учёбы

Презентации

Супер-решатель

Для докладов

Карта сайта

Проверь себя

Для учёбы	Презентации	Супер-решатель
Для докладов	Карта сайта	Проверь себя

Как найти квадратный корень из произведения

Разбор примера

Вычислить:
1) √49 · 25 = √49 · √25 = 7 · 5 = 35

4)√256 · 0,25 · 81 =
= √256 · √0,25 · √81 =
= 16 · √0,25 · √81 = …

Вспомнить порядок извлечения квадратного корня из десятичной дроби √0,25 можно в уроке «Что такое квадратный корень», а правила умножения десятичных дробей в уроке «Умножение десятичных дробей».

√256 · 0,25 · 81 = √256 · √0,25 · √81 =
= 16 · √0,25 · √81 = 16 · 0,5 · 9 =
= 8 · 9 = 72

Разбор примера

Вычислить:
2) √10 · √90 = …

Используем для решения обратное свойство квадратного корня из произведения.

√a · √b = √a · b

---

5)

1 2

  ·

2 3

  · √3 =

1 2

·

2 3

·

3

= …

Для дальнейшего решения применим правила умножения обыкновенных дробей.

1 2

  ·

2 3

  · √3 =
=

1 2

·

2 3

·

3

=

1 2

·

2 3

·

3 1

=
=

1 · 2 · 3 2 · 3 · 1

= …

Сократим полученную дробь под корнем.

… =

1 · 2 · 3 2 · 3 · 1

=

1 · 2 · 3 2 · 3 · 1

= √1 = 1

Квадратный корень из единицы равен единице √1 = 1.

Внимание: частая ошибка!
Неправильное использование квадратного корня из произведения

Разберёмся по традиции на примере. Требуется вычислить.

√82 ² − 18 ² = …

После изучения формулы корня из произведения первым желанием является сделать так:

√82 ² − 18 ² ≠ √82 ² − √18 ²    — неверно

Это неверно. Свойство
   «√a · b = √a · √b »    НЕЛЬЗЯ использовать в данном примере, т.к. под корнем есть знак вычитания «−», т.е. действие вычитания.

Выполним последовательно действия под корнем и вычислим из полученного результата квадратный корень.

√82 ² − 18 ² = √6724 − 324 = √6400 =
= 80

Подобные примеры можно решать другим способом через формулу разности квадратов.

(a² − b²) = (a − b)(a + b)

√82 ² − 18 ² = √(82 − 18)(82 + 18) =
= √64 · 100 = …

Обратите внимание, что сейчас под знаком корня осталось только произведение. Следовательно, мы можем применить свойство корня из произведения.

√a · b = √a · √b

√82 ² − 18 ² = √(82 − 18)(82 + 18) =
= √64 · 100 = √64 · √100 = 8 · 10 = 80

Мы получили такой же результат, как и в первом варианте решения.

Разбор примера

2) √0,01 · 169 = √0,01 · √169 =
= √0,01 · 13 = …

Снова требуется вспомнить правило извлечения квадратного корня из десятичной дроби и умножение десятичных дробей.

√0,01 · 169 = √0,01 · √169 =
= √0,01 · 13 = 0,1 · 13 = 1,3

Разбор примера

6)

2 5

  ·

5 7

  ·

7 8

=
=

2 5

·

5 7

·

7 8

=

2 · 5 · 7 5 · 7 · 8

=
=

2 · 5 · 7 5 · 7 · 84

=

1 4

=

1

2

Разбор примера

1) (√8 + √2)² = …

Для решения примера используем формулу квадрат суммы.

(a + b)² = a² + 2ab + b²

(√8 + √2)² =
= (√8)² + 2 · √8 · √2 + (√2)² =
= 8 + 2 · √8 · 2 + 2 = 10 + 2 · √16 =
= 10 + 2 · 4 = 10 + 8 = 18

---

4) (5√2 + 2√5)(5√2 − 2√5) = …

Обратите внимание, произведение в скобках похоже на формулу «Разность квадратов» в обратном порядке.

(a² − b²) = (a − b)(a + b)
(a − b)(a + b) = (a² − b²)

Действительно, если заменить в формуле «a» на «5√2» и «b» на «2√5», то получится формула сокращенного умножения «Разность квадратов».

(a − b)(a + b) = (a² − b²)

(5√2 + 2√5)(5√2 − 2√5) =
= (5√2)² − (2√5)² = …

Используем свойство «Степень произведения».

(a · b)² = a² · b²

(5√2 + 2√5)(5√2 − 2√5) =
= (5√2)² − (2√5)² =
= 5² · (√2)² − 2² · (√5)² =
= 25 · 2 − 4 · 5 = 50 − 20 = 30

---

Ваши комментарии

Оставить комментарий:

Отправить

---