Скрыть меню

Войти при помощи

Темы уроков

Начальная школа

Математика 5 класс

Математика 6 класс

Алгебра 7 класс

Геометрия 7 класс

Алгебра 8 класс

Алгебра 9 класс

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Начинайте раньше, чем вам кажется нужным. Стив Круг

на главную

Свойства степени

Поддержать сайт

Для учёбы

Презентации

Супер-решатель

Для докладов

Карта сайта

Проверь себя

Для учёбы	Презентации	Супер-решатель
Для докладов	Карта сайта	Проверь себя

Что такое степень числа Свойства степени Возведение в степень дроби

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1
Произведение степеней

Запомните!

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a^m · aⁿ = a^{m + n}, где «a» — любое число, а «m», «n» — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Примеры.

Упростить выражение.
b · b² · b³ · b⁴ · b⁵ = b ^{1 + 2 + 3 + 4 + 5} = b¹⁵
Представить в виде степени.
6¹⁵ · 36 = 6¹⁵ · 6² = 6¹⁵ · 6² = 6¹⁷
Представить в виде степени.
(0,8)³ · (0,8)¹² = (0,8)^{3 + 12} = (0,8)¹⁵

Важно!

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями. Оно не относится к их сложению.

Нельзя заменять сумму (3³ + 3²) на 3⁵. Это понятно, если
посчитать (3³ + 3²) = (27 + 9) = 36 , а 3⁵ = 243

Свойство № 2
Частное степеней

Запомните!

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

a^m

aⁿ

= a^{m − n}, где «a» — любое число, не равное нулю, а «m», «n» — любые натуральные числа такие, что «m > n».

Примеры.

Записать частное в виде степени
(2b)⁵ : (2b)³ = (2b)^{5 − 3} = (2b)²
Вычислить.
11³ · 4 ²
11² · 4
= 11^{3 − 2} · 4 ^{2 − 1} = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3⁸ : t = 3⁴

t = 3⁸ : 3⁴

t = 3^{8 − 4}

t = 3⁴

Ответ: t = 3⁴ = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение.
4^{5m + 6} · 4^{m + 2} : 4^{4m + 3} = 4^{5m + 6 + m + 2} : 4^{4m + 3} = 4^{6m + 8 − 4m − 3} = 4^{2m + 5}
Пример. Найти значение выражения, используя свойства степени.

512 · 4
32
=
512 · 4
32
=
2⁹ · 2²
2⁵
=
2^{9 + 2}
2⁵
=
2¹¹
2⁵
= 2^{11 − 5} = 2 ⁶ = 64

Важно!

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4³ −4²) на 4¹. Это понятно, если посчитать (4³ −4²) = (64 − 16) = 48, а 4¹ = 4

Будьте внимательны!

Свойство № 3
Возведение степени в степень

Запомните!

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(aⁿ)^m = a^{n · m}, где «a» — любое число, а «m», «n» — любые натуральные числа.

Пример.
(a⁴)⁶ = a^{4 · 6} = a²⁴
Пример. Представить 3²⁰ в виде степени с основанием 3².

По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:

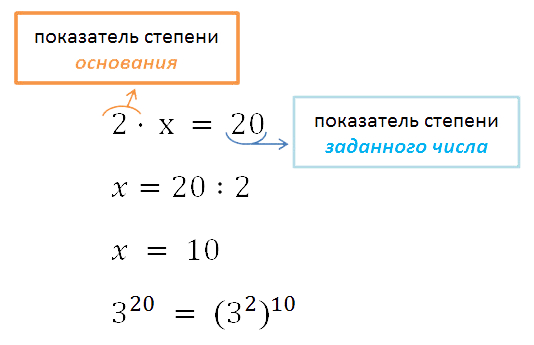
Свойства 4
Степень произведения

Запомните!

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)ⁿ = aⁿ · bⁿ, где «a», «b» — любые рациональные числа; «n» — любое натуральное число.

Пример 1.
(6 · a² · b³ · c )² = 6² · a^{2 · 2} · b^{3 · 2} · с ^{1 · 2} = 36 a⁴ · b⁶ · с ²
Пример 2.
(−x² · y)⁶ = ( (−1)⁶ · x^{2 · 6} · y^{1 · 6}) = x¹² · y⁶

Важно!

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

(aⁿ · bⁿ)= (a · b) ⁿ

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

Пример. Вычислить.
2⁴ · 5⁴ = (2 · 5)⁴ = 10⁴ = 10 000
Пример. Вычислить.
0,5¹⁶ · 2¹⁶ = (0,5 · 2)¹⁶ = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

Например, 4⁵ · 3² = 4³ · 4² · 3² = 4³ · (4 · 3)² = 64 · 12² = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4²¹ · (−0,25)²⁰ = 4 · 4 ²⁰ · (−0,25) ²⁰ = 4 · (4 · (−0,25))²⁰ = 4 · (−1)²⁰ = 4 · 1 = 4

Свойства 5
Степень частного (дроби)

Запомните!

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)ⁿ = aⁿ : bⁿ, где «a», «b» — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5 : 3)¹² = 5¹² : 3¹²

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.