На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Длина окружности
Поддержать сайтВозьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
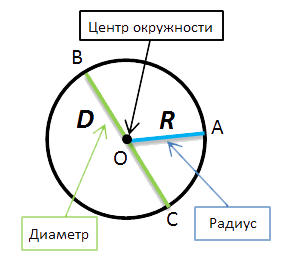
- (·)O — называется центром окружности.
- Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности. Радиус окружности обозначается буквой «R». На рисунке выше — это отрезок «OA».
- Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.
Диаметр окружности обозначается буквой «D». На рисунке выше — это отрезок «BC».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,
округленное до разряда сотых
π ≈ 3,14…
Теперь, зная, что такое число π, мы можем записать формулу длины окружности.
Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Разбор примера
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
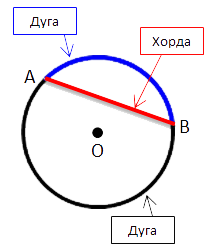
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга «AB» и черная дуга «AB». Точки «A» и «B» называют концами дуг.
Соединим точки «A» и «B» отрезком. Полученный отрезок называют хордой.

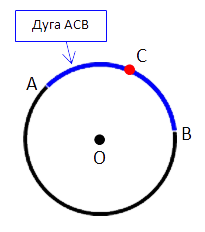
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Владислав Заступневич
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=
| 1 |
| 3 |
 Ответить
Ответить
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12м
 Ответить
Ответить
Ответ для Вика Камалова
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м
 Ответить
Ответить
| плиз |
| плиз |
 Ответить
Ответить
Ответ для Вика Камалова
 Ответить
Ответить
Я не понимаю как найти площадь круга.
 Ответить
Ответить
 Ответить
Ответить
Ответ для Игорь Желтоновский
Площадь круга(S) вычисляется по формуле: S=?r2
Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,12=13,8474
Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php
 Ответить
Ответить











