На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Как решать задачи на функцию
Поддержать сайт«y = kx + b» и её график Как построить график функции вида
«y = 7» или «x = 2»
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».
После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание. Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором значение «y» равно «−19».
Для того, чтобы вычислить «y» при «x = 15» достаточно подставить в функцию вместо «x» необходимое числовое значение.
Запись решения выглядит следующим образом.
Для того, чтобы найти «x» по известному «y», необходимо подставить вместо «y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x» мы подставляем в функцию «y = 2x − 1» вместо «y» число «−19» .
Мы получили линейное уравнение с неизвестным «x», которое решается по правилам решения линейных уравнений.
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный.
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на «−1» для смены знака.
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание. Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство «f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x» числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать правило знаков.
Неправильно

Правильно

С помощью расчетов мы получили «f(−2) = 12».
Это означает, что «f(−2) = −18» для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси «Ox» вместо «x» и координату по оси «Oy» вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6» координаты точки (1; 2).
Вместо «x» подставим «1». Вместо «y» подставим «2».
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0». Вместо «y» подставим «1».
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции «y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график мы уже строили в предыдущем уроке.

Найдем на графике функции «y(x) = −2x + 1», чему равен «y» при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».

Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции «y(x) = −2x + 1». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3.
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
«y = kx + b» и её график Как построить график функции вида
«y = 7» или «x = 2»
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
f(x2-3x)=3x2+5x-4
f(3)=?
 Ответить
Ответить
у=3х-5 при каком значении аргумента значение функции раво 10
 Ответить
Ответить
Ответ для Иван Баранов
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
 Ответить
Ответить










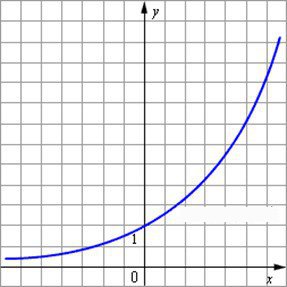 определите вид графика
определите вид графика

