На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Решение сложных уравнений. 5 класс
Поддержать сайтПод сложными (составными) уравнениями мы понимаем уравнения, которые содержат два или более арифметических действия.
Решение таких уравнений выполняется по тем же правилам, которые мы рассмотрели на странице «Решение простых уравнений 5 класс» в этой же теме.
Но решение составных уравнений производится в определённой последовательности.
Рассмотрим уравнение:
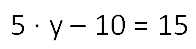
- Расставляем порядок действий в уравнении.
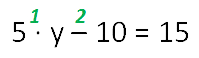
- Определяем неизвестное по последнему действию. Последнее действие в данном уравнении
— это вычитание.
Обращаем ваше внимание, что на этом этапе наше неизвестное — это «5y», и именно его
мы рассматриваем как уменьшаемое.
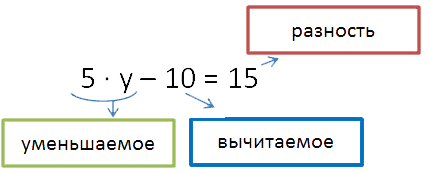
- Решаем как простое уравнение и находим «5y». Вспомним правило для нахождения неизвестного уменьшаемого.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
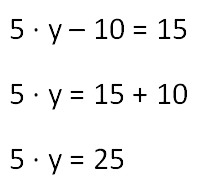
- Теперь перед нами простое уравнение. Необходимо найти неизвестный множитель. Решаем
уравнение по следующему правилу.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
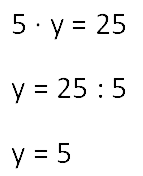
- Не забудем выполнить проверку.
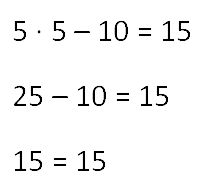
Всё верно. Значит уравнение решено правильно.
Другой способ решения сложных уравнений
Некоторые сложные (составные уравнения) можно решать другим способом. Зная и умея применять свойства сложения и вычитания, а также свойства умножения и деления, уравнения решаются следующем образом.
Рассмотрим уравнение.
- Упрощаем выражение, стоящее в левой части уравнения, используя одно из свойств вычитания.
Чтобы из суммы отнять число, нужно это число вычесть из одного слагаемого и прибавить результат вычитания к другому слагаемому.
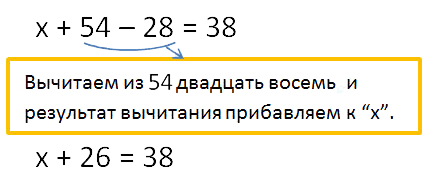
- Далее решаем простое уравнение, пользуясь правилом нахождения неизвестного слагаемого.
x = 38 − 26
x = 12 - Выполняем проверку.
(12 + 54) − 28 = 38
66 − 28 = 38
38 = 38
Упрощение выражений в уравнениях
Если в уравнении встречается выражения, которые можно упростить, то вначале упрощаем выражения, и только после этого решаем уравнение.
Решить уравнение.
Левую часть уравнения можно упростить. Сделаем это.
Теперь решим простое уравнение по правилу нахождения неизвестного множителя.
x = 7
Завершив пример, выполним проверку.
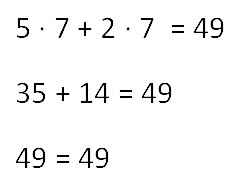
Ваши комментарии
Оставить комментарий:
3)(y-4)*2+10y=
4)(2y+5)*4-11y=
5)4x+2(0.5x+3)=
6)6x-3(x-7)=
 Ответить
Ответить
Ответ для Асико Абишов
2)5(4-3х)+8х=20-15х+8х=-7х+20
3)(у-4)2+10у=2у-8+10у=12у-8
4)(2у+5)4-11у=8у+20-11у=-3у+20
5)4х+2(0.5х+3)=4х+1х+6=5х+6
6)6х-3(х-7)=6х-3х+21=3х+21
 Ответить
Ответить
 Ответить
Ответить
Ответ для Трофим Сидорченко
х+х=100+9,8
2х=109,8
х=109,8:2
х=54,9 тонн угля на втором складе
на первом складе 54,9-9,8=45,1 тонн угля
на двух 54,9+45,1=100 тонн
Ответ: на первом складе 45,1 тонн угля, на втором складе 54,9 тонн угля.
 Ответить
Ответить
| 1 |
| 2 км |
| 2 |
| 3 |
 Ответить
Ответить
Ответ для Елизавета Сигорская
| 1 |
| 2 км |
13,5- 1 час
| 2 |
| 3 |
13,5: 3 * 2 = 9 км.
Ответ: 9 км.
 Ответить
Ответить