На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Золотое сечение в математике
Поддержать сайтКрасота, оказывается, порою имеет математическое объяснение. Пропорции золотого сечения часто используются художниками и скульпторами в соотношениях между разными элементами картины или скульптуры. Великий Леонардо да Винчи находил соотношение золотого сечения в пропорциях человеческого тела.
Так чему же равно отношение золотого сечения в математике и как его найти? Разберёмся на примере.
Возьмём лист бумаги и начертим линию горизонта, которая обычно делит небо от земли. Получится, нечто похожее на рисунок ниже.
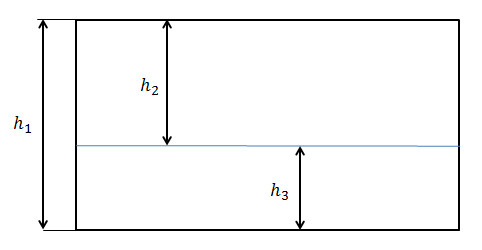
Отношение высоты картины h1 к расстоянию от верхнего края h2 равно отношению расстояния от верхнего края h2 к расстоянию до нижнего края h3. В виде математической записи, это будет выглядеть так:
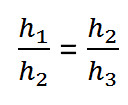
Найдём числовое значение золотого сечения.
Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна h1 = 1, а расстояние от верхнего края до горизонта обозначим за x (h2 = x). Тогда получим:
| 1 |
| x |
| x |
| (1 − x) |
x2 + x − 1 = 0
Положительный корень этого уравнения
| (√5 + 1) |
| 2 |
Это отношение большей части к меньшей в этой пропорции.
Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами τ (тау) или φ (фи). Другие греческие буквы вы можете посмотреть в разделе «Для учёбы».
Золотое сечение в фигурах
В некоторых фигурах геометрии и стереометрии также присутствует золотое сечение. Например, в пятиконечной звезде (пентаграмме).
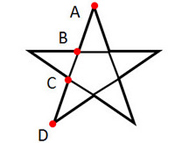
Точка «B» или «С» делит отрезок «AD» в пропорциях золотого сечения. Все остальные стороны звезды также поделены в данном соотношении соответственно.
Другой пример золотого сечения был обнаружен в пирамиде Хеопса.

В сечении знаменитого сооружения также заложен принцип золотого сечения.
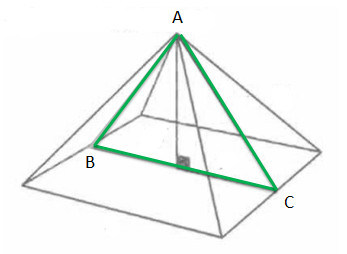
Сумма двух сторон равнобедренного треугольника «ABC» относится к его основанию также как сумма всех сторон треугольника к сумме равных сторон. Иными словами:
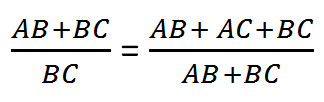
Ваши комментарии
Оставить комментарий: