На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Как решать задачи на квадратичную функцию
Поддержать сайтВ предыдущем уроке мы подробно разобрали, как построить параболу. В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y» число ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции
Подставим в исходную функцию вместо «y» ноль и решим полученное квадратное уравнение.
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| ± √12 |
| 2 |
x1;2 =
| ± √4 · 3 |
| 2 |
x1;2 =
| ± 2√3 |
| 2 |
x1;2 = ±√3
| x1 = √3 | x2 = −√3 |
Ответ: нули функции «y = x2 − 3» :
Как найти при каких значениях «x» квадратичная функция принимает заданное числовое значение
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение, нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
Подставим в исходную функцию
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
| 1 ± √1 |
| 2 |
x1;2 =
| 1 ± 1 |
| 2 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение
Как найти координаты точек пересечения параболы и прямой
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x» в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2» и прямой «y = 3 − 2x».
Приравняем правые части функций и решим полученное уравнение относительно «x».
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| −2 ± √4 + 12 |
| 2 |
x1;2 =
| −2 ± √16 |
| 2 |
x1;2 =
| −2 ± 4 |
| 2 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси «Ox» вместо «x», а координату по оси «Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
Подставим в функцию «y = x2» координаты точки (·) А(2; 6).
6 = 22
6 = 4 (неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
Подставим в функцию «y = x2» координаты точки (·) B(−1; 1).
1 = (−)12
1 = 1 (верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
Сначала определим точки пересечения функции с осью «Ox». На графике функции эти точки выглядят так:
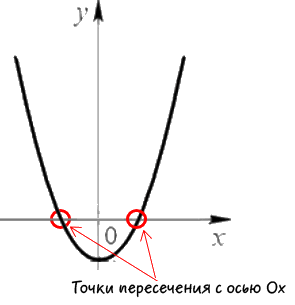
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox» равна нулю, поэтому подставим «y = 0» в исходную функцию «y = x2 −3x + 2» и найдем их координаты по оси «Ox».
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
| 3 ± √9 − 8 |
| 2 |
x1;2 =
| 3 ± √1 |
| 2 |
x1;2 =
| 3 ± 1 |
| 2 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
Теперь найдем координаты точки пересечения с осью «Oy».
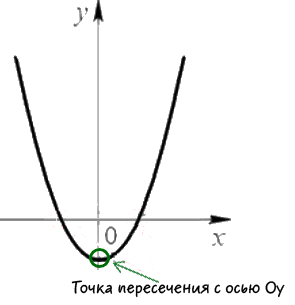
Как видно на рисунке выше, координата «x» точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0» в исходную функцию «y = x2 −3x + 2» и найдем координату точки по оси «Oy».
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает положительные или отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает значения» — речь идет о значениях«y». Другими словами, необходимо ответить на вопрос: при каких значениях «x», координата «y» положительна или отрицательна.
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения;
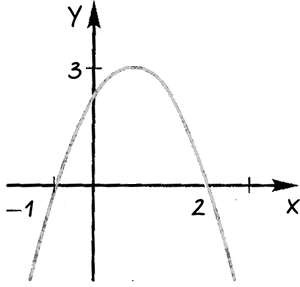
Проведем через точки, где график функции пересекает ось «Ox» прямые.
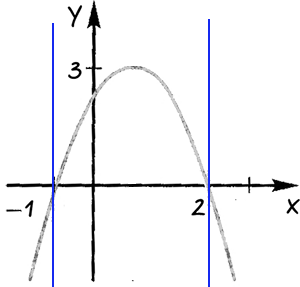
Определим области, где функция принимает отрицательные или положительные значения.
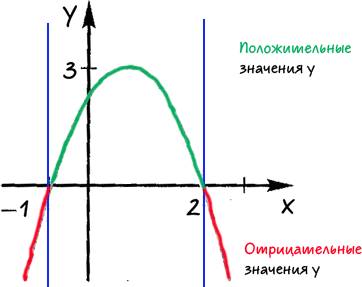
Подпишем над каждой полученной областью, какие значения принимает «x» в каждой из выделенных областей.
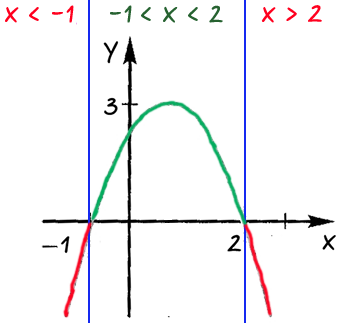
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при
Ваши комментарии
Оставить комментарий: