На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Задача на растворы
Поддержать сайтДля того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.
Концентрация раствора — это часть, которую составляет масса растворённого вещества от массы всего раствора.
- 9%-я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.
Разбор примера
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
- 1 кг — масса растворённого вещества (соли)
- 9 кг — масса воды в растворе (не путать с общей массой раствора)
- 9 + 1 = 10 кг — общая масса раствора.
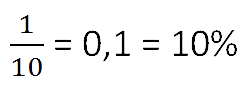
Ответ: 10% — концентрация раствора.
Разбор примера
Теперь решим обратную задачу.
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.
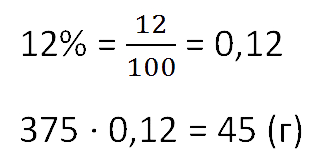
Ответ: 45 г соли.
Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а за «y» массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
Изобразим графически условия задачи.
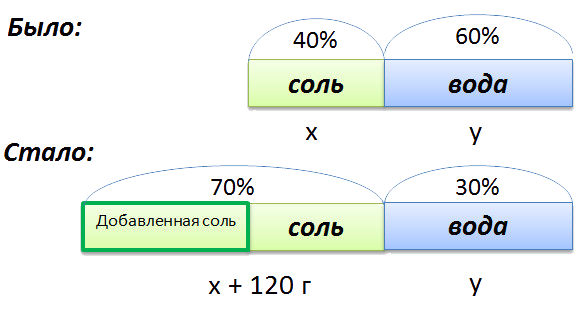
Составим пропорцию, связывающую эти величины до добавления соли.
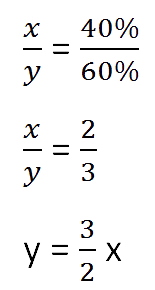
Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе «y».
Выразим её, учитывая изменения в растворе после добавления соли.
- (x + 120) г — масса соли в новом растворе
- (100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.
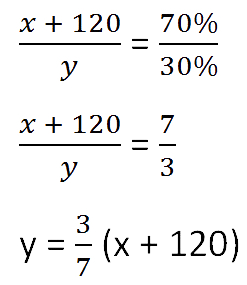
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.
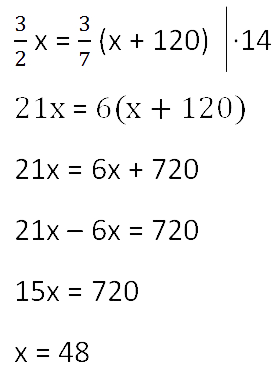
Ответ: 48 г — масса соли в первоначальном растворе.
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Роман Роршахов
 Ответить
Ответить
Ответ для Дарья Сидорова
| 37 |
| 3 |
| 31 |
| 4 |
| 6 |
| 11 |
| 37 |
| 3 |
| 186 |
| 44 |
| 37 · 22 — 3 · 93 |
| 66 |
| 814-279 |
| 66 |
| 535 |
| 66 |
| 7 |
| 66 |
 Ответить
Ответить
 Ответить
Ответить
Ответ для Амина Загребельная
А именно: «Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.»
5: 100=0,05=
| 1 |
| 20 |
 Ответить
Ответить