На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Сложение отрицательных чисел
Поддержать сайтСложение положительных и отрицательных чисел можно разобрать с помощью числовой оси.
Сложение чисел с помощью координатной прямой
Сложение небольших по модулю чисел удобно выполнять на координатной прямой, мысленно представляя себе как точка, обозначающая число передвигается по числовой оси.
Возьмём какое-нибудь число, например, 3. Обозначим его на числовой оси точкой «A».
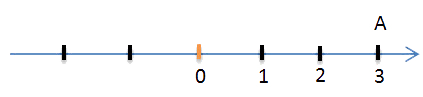
Прибавим к числу положительное число 2. Это будет означать, что точку «A» надо переместить на два единичных отрезка в положительном направлении, то есть вправо. В результате мы получим точку «B» с координатой 5.
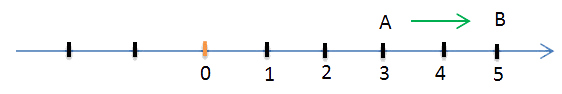
Для того чтобы к положительному числу, например, к 3 прибавить отрицательное число «−5», точку «A» надо переместить на 5 единиц длины в отрицательном направлении, то есть влево.
В этом случае координата точки «B» равна — «2».

Итак, порядок сложения рациональных чисел с помощью числовой оси будет следующим:
- отметить на координатной прямой точку «A» с координатой равной первому слагаемому;
- передвинуть её на расстояние, равное модулю второго слагаемого в направлении, которое соответствует знаку перед вторым числом (плюс — передвигаем вправо, минус — влево);
- полученная на оси точка «B» будет иметь координату, которая будет равна сумме данных чисел.
Пример.
Двигаясь от точки — 2 влево (так как перед 6 стоит знак минус), получим — 8.
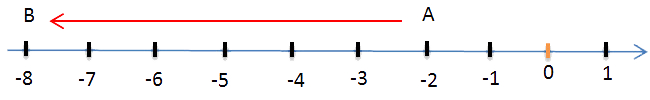
Сложение чисел с одинаковыми знаками
Складывать рациональные числа можно проще, если использовать понятие модуля.
Пускай нам нужно сложить числа, которые имеют одинаковые знаки.
Для этого, отбрасываем знаки чисел и берём модули этих чисел. Сложим модули и перед суммой поставим знак, который был общим у данных чисел.
Пример.
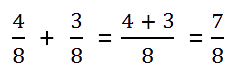
Пример сложения отрицательных чисел.
Чтобы сложить числа одного знака надо сложить их модули и поставить перед суммой знак, который был перед слагаемыми.
Сложение чисел с разными знаками
Если числа имеют разные знаки, то действуем несколько по-иному, чем при сложении чисел с одинаковыми знаками.
- Отбрасываем знаки перед числами, то есть берём их модули.
- Из большего модуля вычитаем меньший.
- Перед разностью ставим тот знак, который был у числа с бóльшим модулем.
Пример сложения отрицательного и положительного числа.
Пример сложения смешанных чисел.
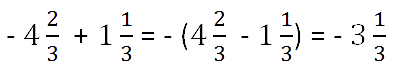
Чтобы сложить числа разного знака надо:
- из бóльшего модуля вычесть меньший модуль;
- перед полученной разностью поставить знак числа, имеющего больший модуль.
Ваши комментарии
Оставить комментарий: