Скрыть меню

Войти при помощи

Темы уроков

Начальная школа

Математика 5 класс

Математика 6 класс

Алгебра 7 класс

Геометрия 7 класс

Алгебра 8 класс

Алгебра 9 класс

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

То, что ты считал вершиной, — только ступенька. Сенека

на главную

Как решить уравнение с неизвестным в дроби

Поддержать сайт

Для учёбы

Презентации

Супер-решатель

Для докладов

Карта сайта

Проверь себя

Для учёбы	Презентации	Супер-решатель
Для докладов	Карта сайта	Проверь себя

Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби

Иногда линейные уравнения принимают вид, когда неизвестное оказывается в числителе одной или нескольких дробей. Как, например, в уравнении ниже.

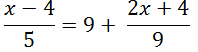
В таких случаях подобные уравнения можно решить двумя способами.

I способ решения
Сведение уравнения к пропорции

Запомните!

При решении уравнений способом пропорции необходимо выполнить следующие действия:

привести все дроби к общему знаменателю и сложить их как алгебраические дроби (в левой и правой части должно остаться только по одной дроби);
полученное уравнение решить по правилу пропорции.

Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны никакие преобразования.

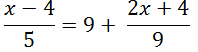
Будем работать с правой частью уравнения. Упростим правую часть уравнения так, чтобы там осталась только одна дробь. Для этого вспомним правила сложения числа с алгебраической дробью.

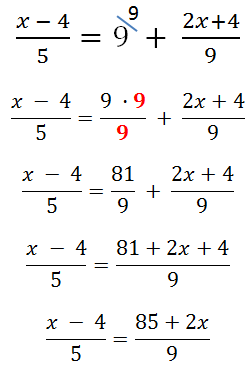
Теперь используем правило пропорции и решим уравнение до конца.

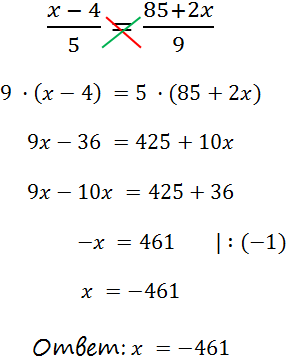
решаем уравнение с неизвестным в дроби как пропорцию

II способ решения
Сведение к линейному уравнению без дробей

Рассмотрим уравнение выше еще раз и решим его другим способом.

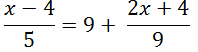Мы видим, что в уравнении присутствуют две дроби «

x − 4

» и «

2x + 4

».

Наша задача сделать так, чтобы в уравнении не осталось ни одной дроби.

Другими словами, необходимо свести уравнение к обычному линейному уравнению без неизвестного в дроби.

Запомните!

Чтобы избавиться от дробей в уравнении нужно:

найти число, которое без остатка будет делиться на каждый из знаменателей;
умножить каждый член уравнения на это число.

Давайте зададим себе вопрос: «Какое число без остатка делится на каждый из знаменателей дробей, то есть и на «5», и на «9» ?». Таким ближайшим наименьшим числом будет число «45».

Умножим каждый член уравнения на «45».

Важно!

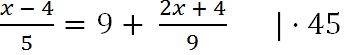
При умножении уравнения на число нужно каждый член уравнения умножить на это число.

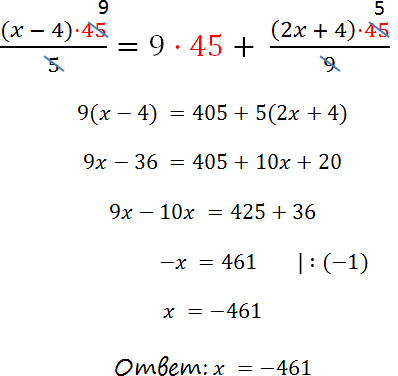
Другие примеры решения уравнений с неизвестным в дроби

Решение уравнения I способом (через пропорцию)

8 − y
5
+
5 − 4y
3
=
y + 6
2

(8 − y) · 3
5 · 3
+
(5 − 4y) · 5
3 · 5
=
y + 6
2

24 − 3y
15
+
25 − 20y
15
=
y + 6
2

24 − 3y + 25 − 20y
15
=
y + 6
2

49 − 23y
15
=
y + 6
2

(49 − 23y) · 2 = 15 · (y + 6)

98 − 46y = 15y + 90

−46y − 15y = 90 − 98

−61y = −8 | :(−61)

y =
8
61

Ответ: y =
8
61

Решение уравнения II способом
(сведение к уравнению без дробей)

2 −
3x − 7
4
+
x + 17
5
= 0 | ·20
2 · 20 −
(3x − 7) · 20
4
+
(x + 17) · 20
5
= 0 · 20

40 − 5 ·(3x − 7) + 4 · (x + 17) = 0

40 − 15x + 35 + 4x + 68 = 0

−15x + 4x + 40 + 35 + 68 = 0

−11x + 75 + 68 = 0

−11x + 143 = 0

−11x = −143 | :(−11)

x = 13
Ответ: x = 13