На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Сокращение дробей
Поддержать сайтС помощью дробей одну и ту же часть целого предмета можно записать разными способами.
На рисунке закрашена половина круга| 1 |
| 2 |
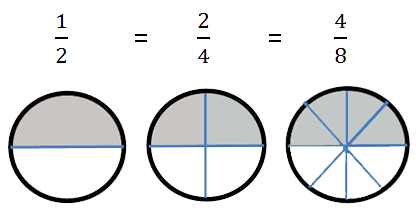 Если этот же круг разделить на 4 части, то
эту же половину круга можно представить как
Если этот же круг разделить на 4 части, то
эту же половину круга можно представить как | 2 |
| 4 |
Если этот же круг разделить на 8 частей, то эту же половину круга можно представить как
| 4 |
| 8 |
Таким образом, все эти дроби равны.
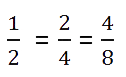 Дробь
Дробь | 2 |
| 4 |
| 1 |
| 2 |
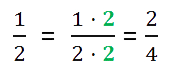
| 4 |
| 8 |
| 1 |
| 2 |
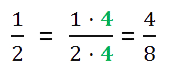
Для удобства дополнительный множитель записывают на наклонной черте справа над дробью.
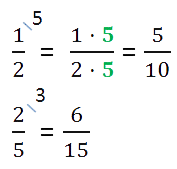
Вернёмся ещё раз к нашим дробям и запишем их в другом порядке.
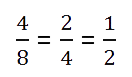
Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.
Такое преобразование дроби называют сокращением дроби.
Сокращение дроби обычно записывают следующим образом.
Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.
Число, на которое делили числитель и знаменатель, держим в уме.
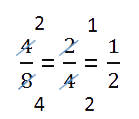
В нашем примере мы сокращали (то есть делили и числитель, и знаменатель) дробь на двойку, которую держали в уме.
Сокращение дроби можно проводить последовательно.
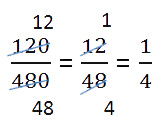
Основное свойство дроби
Сформулируем основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Запишем это свойство в виде буквенных выражений.
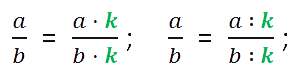 , где «a», «b» и «k» — натуральные числа.
, где «a», «b» и «k» — натуральные числа. Ваши комментарии
Оставить комментарий: