На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Признак делимости на 11
Поддержать сайтна 2, 4 и 8 Признаки делимости
на 3, 6 и 9 Признаки делимости
на 5, 25 и 10 Признак делимости на 11
Существует и другие признаки делимости кроме перечисленных, но они на порядок сложнее. Для тех, кому интересно, приводим пример признака делимости на 11.
Признак делимости на 11
Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.
В самом деле признак делимости на 11 очень интересен, попробуем разобраться на примере:
- Проверим, делится ли 671 на 11.
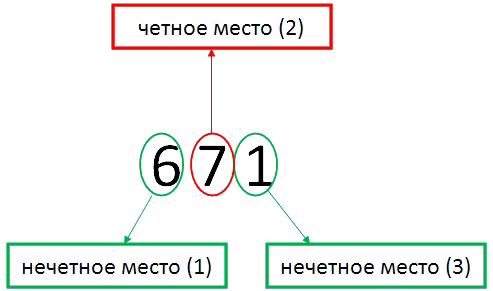
Итак, цифры которые стоят на нечетных местах — это 6 (стоит на первом месте) и 1 (стоит на третьем месте). Цифра, которая стоит на четном месте, это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11.
- Проверим делится ли 3905 на 11 .
Цифры которые стоят на нечетных местах — это 3 (стоит на первом месте) и 0 (стоит на третьем месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте).
3 ≠ 14
Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11, т.к. 14 − 3 = 11. Значит 3905 делится на 11.
Уточнение для признака делимости на 11
На самом деле, правило, описанное выше — это упрощенная версия полного признака делимости на 11. В большинстве случаев при решении задач школьного курса математики его достаточно.
Но если быть точным, признак делимости звучит следующим образом.
Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, которое делится на 11.
Разберемся на примере.
- Проверим, делится ли число 90 904 на 11 без остатка.
- Вычислим сумму цифр на нечетных местах:
9 + 9 + 4 = 22
- Сумма цифр на четных местах:
0 + 0 = 0
- Вычислим разницу между суммами цифр, которые стоят на нечетных и четных местах.
22 − 0 = 22
- Проверим, делится ли число 22 на 11 без остатка.
22 : 11 = 2
- Значит число 90 904 делится на 11 без остатка.
на 2, 4 и 8 Признаки делимости
на 3, 6 и 9 Признаки делимости
на 5, 25 и 10 Признак делимости на 11
Ваши комментарии
Оставить комментарий: