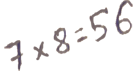На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Что такое
квадратный корень
Поддержать сайтВ уроке «Степень числа» мы проходили, что возвести в квадрат число означает умножить число на само себя. Кратко запись числа в квадрате выглядит следующим образом:
Но как быть, если нам нужно получить обратный результат? Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Нахождение исходного числа, которое в квадрате дало бы требуемое, называется извлечением квадратного корня.
Извлечение квадратного корня — это действие, обратное возведению в квадрат.
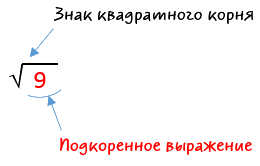
У квадратного корня есть специальный знак. Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9», это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический». Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.
Число под знаком корня называют подкоренным выражением.
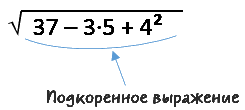
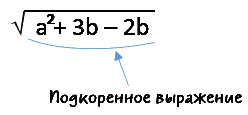
Подкоренное выражение может быть представлено не только одним числом. Всё, что находится под знаком корня, называют подкоренным выражением. Оно может сожержать как числа, так и буквы.
Извлекать квадратный корень можно только из положительного числа.
- √−9 = … нельзя извлекать квадратный корень из отрицательного числа;
- √64 = 8
- √−1,44 = … нельзя извлекать квадратный корень из отрицательного числа;
- √256 = 16
Квадратный корень из нуля
Квадратный корень из нуля равен нулю.
Квадратный корень из единицы
Квадратный корень из единицы равен единице.
Как найти квадратный корень из числа
Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто. Для этого достаточно выучить таблицу квадратов.
Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от 1 до 20.
Решение примеров с квадратными корнями
Разбор примера
Вычислить арифметический квадратный корень из числа.
- √81 = 9
- √64 = 8
- √100 = 10
Как найти квадратный корень из десятичной дроби

При нахождении квадратного корня из десятичной дроби нужно выполнить следующие действия:
- забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
- вычислить для целого числа квадратный корень;
- полученное целое число заменить на десятичную дробь (поставить запятую исходя из правила умножения десятичных дробей).
Более подробно разберем на примере ниже.
Разбор примера
Вычислить квадратный корень из десятичной дроби «0,16».
√0,16 =По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «16».
Нетрудно вспомнить, какое число в квадрате дает «16». Это число «4».
√16 = 4√0,16 = …
Вспомним правило умножения десятичных дробей. Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой дроби.
Т.е., например, при умножении «0,15» на «0,3» в полученном произведении будет десятичная дробь с тремя знаками после запятой.
0,15 · 0,3 = 0,045Значит, при вычислении квадратного корня √0,16 нам нужно найти десятичную дробь, у которой был бы только один знак после запятой. Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться два знака после запятой, как у десятичной дроби «0,16».
Получается, что ответ — десятичная дробь «0,4».
Убедимся, что квадрат десятичной дроби «0,42» дает «0,16». Умножим в столбик «0,4» на «0,4».
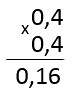
Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:
√1,44 =Представим вместо десятичной дроби «1,44» целое число «144». Какое число в квадрате даст «144»? Ответ — число «12».
122 = 144√144 = 12
√1,44 = …
Так как в десятичной дроби «1,44» — два знака после запятой, значит в десятичной дроби, которая дала в квадрате «1,44» должен быть один знак после запятой.
√1,44 = 1,2Убедимся, что «1,22» дает в квадрате «1,44».
1,22 = 1,2 · 1,2 = 1,44Квадратные корни из чисел √2, √3, √5, √6, и т.п.
Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен √2 или √3 и т.п.
В самом деле, какое число в квадрате даст «2»? Или число «3»? Такое число не будет целым. Более того, оно представляет из себя непериодическую десятичную дробь и входит в множество иррациональных чисел.
Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:
√15 − 2 · 4 = √15 − 8 = √7Нет такого целого числа, которое бы дало в квадрате число «7». Поэтому, перед завершением задачи внимательно читайте её условие.
Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно оставить с корнем.
√15 − 2 · 4 = √15 − 8 = √7Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора, то после вычисления квадратного корня на калькуляторе округлите результат до необходимого количества знаков.
Текст задания в таком случае может быть написан следующим образом:
«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до «0,001».
√15 − 2 · 4 = √15 − 8 = √7 ≈ 2,646Ваши комментарии
Оставить комментарий:
??28-16?3 ( то есть выражение 28-16?3 еще под двумя корнями, не только 28, а все выражение!)
 Ответить
Ответить
Ответ для Temur Uldashev
Скобки не знешь?
 Ответить
Ответить
Ответ для Temur Uldashev
 Ответить
Ответить
Ответ для Temur Uldashev
Спасибо скажи, что тебе подсказали.
 Ответить
Ответить
Ответ для Ксюша Новикова
 Ответить
Ответить
 Ответить
Ответить
Ответ для Макс Простов
?19 ? 4,35
?13 ? 3,61
3 · 4 = 12
7 · 4,35 = 30,45
8 · 3,61 = 28,88
Ответ: 3?16, 8?13, 7?19
 Ответить
Ответить