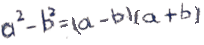На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Упрощение выражений
Поддержать сайтСвойства сложения, вычитания, умножения и деления полезны тем, что позволяют преобразовывать суммы и произведения в удобные выражения для вычислений. Научимся, как можно с помощью этих свойств упрощать выражения.
Вычислим сумму:
В этом выражении есть числа, при сложении которых получаются «круглые» числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения.
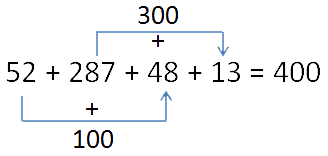
Также для упрощения вычисления произведений можно использовать переместительный закон умножения.
Сочетательные и переместительные свойства используются и при упрощении буквенных выражений.
- 6 · a · 2 = 6 · 2 · a = 12a
- 2 · a · 4 · b = 2 · 4 · a · b = 8ab
- 5b + 8b = (5 + 8) · b = 13b
- 14y − 12y = (14 − 12) · y = 2y
Распределительный закон умножения часто применяется для упрощения вычислений.

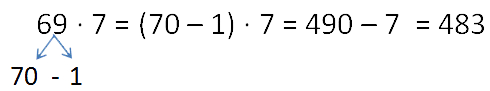
Применяя распределительное свойство умножения относительно сложения или вычитания к выражению «(a + b) · с и (a − b) · c», мы получаем выражение, не содержащее скобки.
В этом случае говорят, что мы раскрыли (опустили) скобки. Для применения свойств не имеет значения, где записан множитель «c» — перед скобками или после.
Раскроем скобки в выражениях.
- 2(t + 8) = 2t + 16
- (3x − 5)4 = 4 · 3x − 4 · 5 = 12x − 20
Если перед буквой не записано число, то подразумевается, что перед буквой стоит числовой множитель 1.
- t + 4t = (1 + 4)t = 5t
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
Получим:
В таких случаях говорят, что из «ac + bc» вынесен общий множитель «с» за скобки.
Примеры вынесения общего множителя за скобки.
- 73 · 8 + 7 · 8 = (73 + 7) · 8 = 80 · 8 = 640
- 7x − x − 6 = (7 − 1)x − 6 = 6x − 6 = 6(x − 1)
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Diana Uralbaeva
 Ответить
Ответить
| y |
| x²-xy |
| 1 |
| x-y |
| x + y |
| x²-xy |
| y |
| xy-y² |
 Ответить
Ответить
Ответ для Александра Воробьёва
| 1 |
| x-y |
| x(x-y) |
| x+y |
| x |
| x+y |
2)
| y |
| x(x-y) |
| y |
| y(x-y) |
| y(y-x) |
| -xy(y-x) |
| 1 |
| -x |
3) —
| 1 |
| x |
| x |
| x+y |
| x+y+x2 |
| x(x+y) |
 Ответить
Ответить
 Ответить
Ответить
Ответ для Сабина Ерназарова
6мин · 15 бревен = 90 минут = 1,5 часа ( в одном часе 60 минут. 90/60 = 1,5)
При времени равным 7 минутам действия совершаются аналогично:
7 минут · 15 бревен = 105 минут = 1,75 часа.
 Ответить
Ответить