На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Рациональные числа
Поддержать сайтРациональные числа — это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).
Есть версия, что название рациональных чисел связано с латинским словом
«ratio» —
разум.
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
Поэтому число «Пи» (π = 3,14...) , основание натурального логарифма
e (e = 2,718..)
или √2 НЕ являются рациональными числами.
Примеры рациональных чисел:
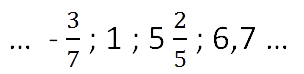
Множество рациональных чисел обозначается заглавной английской буквой «Q» (кью).
Множество «Q» включает в себя множество целых чисел «Z» и натуральных чисел «N».
 Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит
целым числам, а знаменатель — натуральным.
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит
целым числам, а знаменатель — натуральным.
| a |
| b |
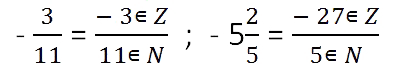
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Артем Камалиев
Что нам это даёт? Произведение в котором учавствует нуль равно нулю. Сумма положительного и отрицательного чисел равна нулю. Соотвественно сумма и произведение равны нулю и равны между собой.
 Ответить
Ответить