На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Квадратные неравенства с одним корнем или без корней
Поддержать сайтПрежде чем перейти к разбору решений не совсем типичных квадратных неравенств, потренируйтесь в
решении обычных квадратных неравенств,
у которых при решении соответствующего квадратного уравнения получаются два корня.
Квадратные неравенства, у которых получается один корень
Рассмотрим неравенство, в котором при решении квадратного уравнения методом интервалов получается только один корень. Например, требуется решить следующее квадратное неравенство:
Используем метод интервалов для решения квадратного неравенства. Сразу переходим к п.3 правила из урока «Метод интвервалов», так как п.1 и п.2 уже выполнены. То есть, приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x1;2 =
| −(−2) ± √(−2)2 − 4 · 1 · 1 |
| 2 · 1 |
x1;2 =
| 2 ± √4 − 4 |
| 2 |
x1;2 =
| 2 ± √0 |
| 2 |
x1;2 =
| 2 |
| 2 |
x1 = x2 = 1
У нас получилось, что оба корня имеют одно одинаковое значение равное единице. Другими словами, значение корня повторяется два раза. Отметим это значение на числовой оси согласно п.5 из правила метода интервалов.
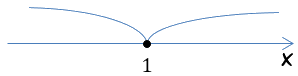
Теперь по п.6 отметим знаки внутри интервалов. Но в отличии от решения обычных квадратных неравенств с двумя различными корнями здесь появляется важный нюанс.
Если значение корня в уравнении повторяется четное количество раз, то при расставлении знаков в интервалах при переходе через этот корень знак не меняется.
В нашем случае значение корня повторяется два раза «x1 = x2 = 1». Значит, при переходе через это значение знак не поменяется. С учетом выше сказанного проставим знаки в интервалах справа налево, начиная со знака «+».
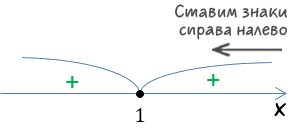
Теперь по исходному неравенству
Таких интервалов на нашем рисунке нет, но неравенство нестрогое, значит, только число «1» является решением неравенства. Запишем ответ.
Ответ: x = 1
Убедимся в правильности нашего решения, подставив «x = 1» в исходное неравенство.
12 − 2 · 1 + 1 ≤ 0
0 ≤ 0 (верно)
Квадратные неравенства, не имеющие корней (нет решений)
Рассмотрим квадратные неравенства, у которых при решении соответствующего квадратного уравнения не получается ни одного корня. Пусть требуется решить следующее квадратное неравенство.
П.1 и п.2 для решения этого квадратного неравенства методом интервалов уже выполнен, поэтому сразу перейдем к п.3, то есть к решению соответсвующего квадратного уравнения.
x2 + 2x + 7 = 0
x1;2 =
| 2 ± √22 − 4 · 7 · 1 |
| 2 · 1 |
x1;2 =
| 2 ± √4 − 28 |
| 2 |
x1;2 =
| 2 ± √−24 |
| 2 |
Нет действительных корней
При решении квадратного уравнения мы получили, что действительных корней нет. Но это вовсе не означает, что исходное квадратное неравенство невозможно решить.
Если при решении квадратного уравнения для неравенства получилось, что действительных корней нет, значит, ответом квадратного неравенства будет: «нет действительных решений».
Так и запишем в ответ.
Ответ: нет действительных решений.
При написании ответа для квадратного неравенства важно помнить, что изначально мы решаем именно неравенство, поэтому речь идет именно о «решениях», а не о «корнях».
Помните, что решением любых неравенств, как правило, являются области решений (множество чисел), а в уравнениях — это конкретные числа, которые мы называем корнями уравнений.
Стоит запомнить для себя: уравнения — корни, неравенства — решения.
В завершении урока разберем еще одно квадратное неравенство, при решении которого получается только один корень.
x2 − 6x + 9 = 0
x1;2 =
| 6 ± √62 − 4 · 1 · 9 |
| 2 · 1 |
x1;2 =
| 6 ± √36 − 36 |
| 2 |
x1;2 =
| 6 ± √0 |
| 2 |
x1;2 =
| 6 ± 0 |
| 2 |
x1;2 =
| 6 |
| 2 |
x1 = x2 = 3
Корень повторяется два раза, значит, знак при переходе через число «3» не меняется.
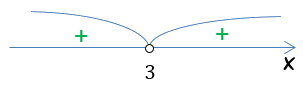
Выберем нужные интервалы. В исходном неравенстве
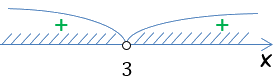 Ответ: x < 3; x > 3
Ответ: x < 3; x > 3
Ваши комментарии
Оставить комментарий: