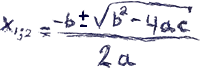На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Квадратные неравенства.
Метод интервалов
Поддержать сайтПрежде чем разбираться, как решать квадратное неравенство, давайте рассмотрим, какое неравенство называют квадратным.
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x» равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
| x − 7 < 0 | линейное |
| x2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x2 + x − 12 ≤ 0 | квадратное |
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать линейные неравенства. Но в отличие от линейных неравенств квадратные решаются совсем иным образом.

Решать квадратное неравенство таким же образом как и линейное нельзя!
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать этот метод и почему он получил такое название.
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
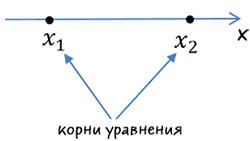
- нарисовать «арки» для интервалов. Справа налево,
начиная с «+», проставить чередуя знаки «+»
и «−»;
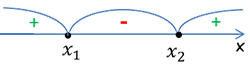
- выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
Итак, согласно п.1 мы должны перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль. В заданном неравенстве «x2 + x − 12 < 0» ничего дополнительно делать не требуется, так как в правой части и так уже стоит ноль.
Переходим к п.2. Необходимо сделать так, чтобы перед «x2» стоял положительный коэффициент. В неравенстве «x2 + x − 12 < 0» при «x2» стоит положительный коэффициент «1», значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √1 + 48 |
| 2 |
x1;2 =
| −1 ± √49 |
| 2 |
x1;2 =
| −1 ± 7 |
| 2 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
| x1 = −4 | x2 = 3 |
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.

Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси разным образом.
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.

Проставим знаки внутри интервалов. Справа налево чередуя, начиная с «+», отметим знаки.
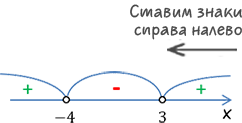
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.
Так как в нашем неравенстве

Отрицательным интервалом оказался лишь один, который находится между числами
«−4» и «3», поэтому
запишем его в ответ в виде двойного неравенства
−4 < x < 3.
Запишем полученный ответ квадратного неравенства.
Ответ: −4 < x < 3
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами, метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 < x < 3 и подставим его вместо «x» в исходное неравенство. Если мы получим верное неравенство, значит мы нашли ответ квадратного неравенства верно.
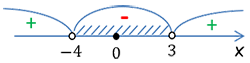
Возьмем, например, из интервала число «0». Подставим его в исходное неравенство «x2 + x − 12 < 0».
02 + 0 − 12 < 0
−12 < 0 (верно)
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √1 + 48 |
| 2 |
x1;2 =
| −1 ± √49 |
| 2 |
x1;2 =
| −1 ± 7 |
| 2 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
| x1 = −4 | x2 = 3 |
 Ответ: −4 < x < 3
Ответ: −4 < x < 3
Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
В правой части неравенство уже стоит ноль. При «x2» стоит «2» (положительный коэффициент), значит можно сразу переходить к поиску корней.
2x2 − x = 0
x1;2 =
| −(−1) ± √(−12) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
| 1 ± √1 |
| 4 |
x1;2 =
| 1 ± 1 |
| 4 |
x1 =
|
x2 =
|
||||
x1 =
|
x2 =
|
||||
x1 =
|
x2 = 0 |
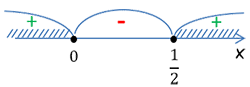 Ответ: x ≤ 0; x ≥
Ответ: x ≤ 0; x ≥ | 1 |
| 2 |
Рассмотрим пример, где перед «x2» в квадратном неравенстве стоит отрицательный коэффициент.
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы перед «x2» стоял положительный коэффициент. Для этого умножим все неравенство на «−1».

Помните, что при умножении неравенства на отрицательное число, знак неравенства меняется на противоположный.
x2 + 3x − 4 ≤ 0
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение. Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x2 + 3x − 4 = 0
x1;2 =
| −3 ± √32 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
| −3 ± √9 + 16 |
| 2 |
x1;2 =
| −3 ± √25 |
| 2 |
x1;2 =
| −3 ± 5 |
| 2 |
x2 =
|
x1 =
|
||||
x2 =
|
x1 =
|
||||
| x2 = −4 | x1 = 1 |
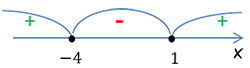

При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это «x2 + 3x − 4 ≤ 0».
Значит для ответа нужно выбирать интервалы со знаком «−».
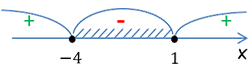 Ответ: −4 ≤ x ≤ 1
Ответ: −4 ≤ x ≤ 1
К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше. Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке «Квадратные неравенства с одним корнем или без корней».
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
(x2+3x+3)x^2 -1<(8x-3)x^2 -1
 Ответить
Ответить
Ответ для Gulnara Muslimova
ac < bc <=> c·ln(a/b) < 0
и метод интервалов.
 Ответить
Ответить