На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Способ группировки
Поддержать сайтКроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.
Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.
Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.
- Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
- Вынести общий множитель за скобки у каждой группы одночленов.
- Вынести полученный общий многочлен за скобки.
Рассмотрим пример разложения многочлена на множители способом группировки.
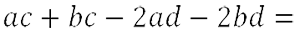
- Подчеркнем повторяющиеся буквенные множители в одночленах.
- Вынесем общий множитель за скобки у каждой группы одночленов.
- Теперь в полученном результате вынесем общий многочлен «(a + b)» за скобки.
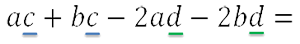

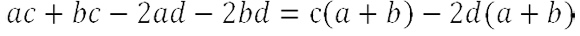 Проверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно.
Проверим, верно ли мы вынесли общий множитель за скобки. Для этого раскроем скобки обратно.
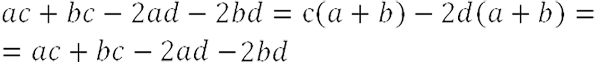 Мы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки.
Мы получили исходный многочлен, значит, мы правильно вынесли общий множитель за скобки.
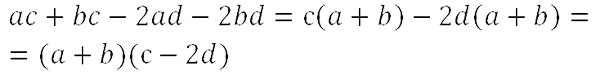
Примеры способа группировки
Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен.
Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.
Первый способ
48xz2 + 32xy2 − 15z2 − 10y2 =Обратим внимание, что в двух одночленах повторяется «y2» и «z2». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.
48xz2 + 32xy2 − 15z2 − 10y2 = 48xz2 − 15z2 + 32xy2 − 10y2 = 3z2(16x − 5) + 2y2(16x − 5) =
= (16x − 5)(3z2 + 2y2)
Второй способ
Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется «x». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.
48xz2 + 32xy2 − 15z2 − 10y2 = 16x(3z2 + 2y2) − 5(3z2 + 2y2) = (3z2 + 2y2)(16x − 5)В итоге получился такой же ответ, как и при первом способе.
Рассмотрим еще один пример разложения многочлена способом группировки.
-
4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1)
= (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1), что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.
Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.
Для этого за скобки выносится знак «−», а в скобках у всех одночленов меняются знаки на противоположные.
2ab2 − 3x + 1 = −(−2ab2 + 3x − 1)
Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потребуется выполнить смену знаков в скобках.
-
2m(m − n) + n − m = −2m(
−m + n) + (n − m) = −2m(n − m) +
1 · (n − m) =
= (n − m)(−2m + 1)
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Pavel Asafov
Да, это тоже рабочий вариант решения задачи.
 Ответить
Ответить