На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Вынесение общего множителя за скобки
Поддержать сайтРазложить многочлен на множители можно несколькими способами. Один из них называется вынесение общего множителя за скобки.
Разложить многочлен на множители — значит представить его в виде произведения двух и более многочленов.
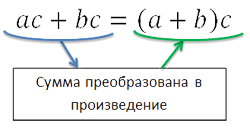
Как вынести общий множитель за скобки
Чтобы вынести общий множитель за скобки нужно выполнить следующие действия.
- Работаем с числовыми коэффициентами.
Находим число, на которое делятся без остатка числовые коэффициенты каждого одночлена. - Работаем с буквенными множителями.
Находим буквенные множители, которые повторяются в каждом одночлене. Выносим их за скобку в наименьшей степени. - Вычисляем многочлен, который остается в скобках.
Рассмотрим пример вынесения общего множителя за скобки.
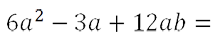
Сначала определим число, на которое без остатка делятся все числовые коэффициенты одночленов. Для этого выпишем все числовые коэффициенты в таблицу ниже.
| Одночлен | Числовой коэффициент | Вывод |
|---|---|---|
| 6a2 | 6 | Все числовые коэффициенты делятся без остатка на число «3». |
| −3a | −3 | |
| 12ab | 12 |
Определим буквенные множители, которые повторяются во всех одночленах.
В многочлене «6a2 − 3a + 12ab» — только буквенный множитель «a» присутствует во всех одночленах. Наименьшая степень буквенного множителя «a» среди всех одночленов — первая.
Теперь перемножим выбранный числовой коэффициент и буквенный множитель.
Получим «3a» и вынесем его за скобки.
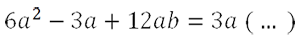
Теперь вычислим оставшийся многочлен в скобках.
Для этого составим таблицу ниже, где будем к каждому одночлену задавать вопрос:
«На что нужно умножить «3а», чтобы получить данный одночлен?»
| Вопрос | Полученный одночлен |
|---|---|
| На что нужно умножить «3а», чтобы получить «6а2»? | На «2а». |
| На что нужно умножить «3а», чтобы получить «−3a»? | На «−1». |
| На что нужно умножить «3а», чтобы получить «12ab»? | На «4b». |
Запишем полученный ответ.
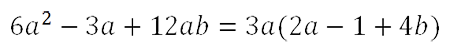

Всегда проверяйте полученный результат вынесения общего множителя.
Для этого раскройте скобки в полученном результате по правилу умножения многочлена на одночлен.
Если вы вынесли общий множитель правильно, то вы должны получить исходный многочлен.
Проверим, правильно ли мы вынесли общий множитель за скобки.
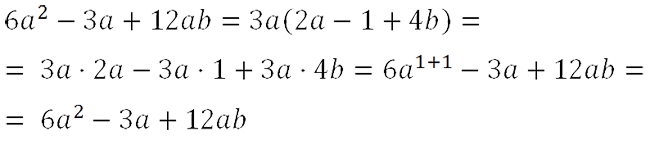
При раскрытии скобок мы получили исходный многочлен, значит мы правильно вынесли общий множитель за скобки.

Действие обратное вынесению общего множителя за скобки называется раскрытием скобок.
Примеры вынесения общего множителя за скобки
-
a4 + 2a2 = a2(a2 + 2)
Проверка: a2(a2 + 2) = a2 · a2 + 2a2 = a2 + 2 + 2a2 = a4 + 2a2
- 2x2y2 − 2x4y2 + 6x3y3 =
2x2y2(1 − x2 + 3xy)
Проверка: 2x2y2(1 − x2 + 3xy) = 2x2y2 · 1 − 2x2y2 · x2 + 2x2y2 · 3xy =
= 2x2y2 − 2x2 + 2 y2 + 6x2 + 1 y2 + 1 = 2x2y2 − 2x4y2 + 6x3y3
Вынесение общего многочлена за скобки
Иногда есть возможность вынести многочлен за скобки целиком.
В таком случае оставшиеся одночлены просто записываются в скобки друг за другом вместе со знаком, который стоял слева от них.
-
a2(x + y) + b3(x + y) = (x + y)(a2 + b3)
— выносим многочлен
(x + y) за скобки.
- a3(x2 + y2) − b(x2 + y2) = (a3 − b)(x2 + y2) — выносим многочлен (x2 + y2) за скобки.
Ваши комментарии
Оставить комментарий: