На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Числовые и буквенные выражения
Поддержать сайтДля правильного решения уравнений нужно уметь пользоваться математическим языком. Словами математического языка являются числовые и буквенные выражения.
Математические выражения могут состоять из одного числа или из одной буквы:
- 42
- z
Или из двух и более чисел и букв, соединённых знаками арифметических действий:
- a − 4
- 2x
- x + y
В записи выражений никогда не применяются знаки равенств и неравенств.
Знаки выше служат для записи равенств и неравенств.
Математические выражения делятся на числовые и буквенные.
Выражение называют числовым, если оно не содержит букв. Примеры числовых выражений:
- 8
- 3 · 4
- 5 : 1
- 41 + 2 · 3
Если выполнить все действия, содержащиеся в числовом выражении, то получится числовое значение выражения.
Пример:
Запись «30 · 5 + 40» — это числовое выражение.
Выполнив все действия, получим число «190» — числовое значение выражения.
Если какое-либо число в числовом выражении заменить буквой, то полученное выражение называют буквенным.
- 7t + 5
- ab − c
- 25:5 − y
Числовой множитель (коэффициент) всегда пишут перед буквой.
Знак умножения между числом и буквой обычно не пишут.
- 3x + 5y
- 5abc
Знак умножения не пишут в тех случаях, когда один из множителей стоит перед или после скобки, или оба множителя выражены буквами.
- 3(t + n)
- xn
Как читаются буквенные выражения
Читаются буквенные выражения следующим образом.
- «4a» − четыре «a»
- Более сложные выражения начинают читать по последнему выполняемому действию. Рассмотрим буквенное
выражение ниже.
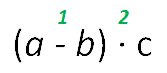 Последнее действе в данном выражении — умножение. Поэтому читаем выражение так:
произведение разности чисел «a» [а] и «b» [бэ] на число «c» [це].
Последнее действе в данном выражении — умножение. Поэтому читаем выражение так:
произведение разности чисел «a» [а] и «b» [бэ] на число «c» [це].
В буквенном выражении строчные латинские буквы могут обозначать различные числа.
Число, которым мы заменяем строчную латинскую букву при расчётах, называется значение буквы в буквенном выражении. В зависимости от задания примера таких значений у одной и той же буквы может быть несколько.
Разбор примера
Найдите значение выражения:
Вместо буквы «a» подставим данные в задании её значения. Сначала первое значение, затем второе.
- 567 + 7 483 = 8 050
- 2 415 + 7 483 = 9 898
Ваши комментарии
Оставить комментарий:
Докажите, что (b+c-2a)(c-b) + (c+a-2b)(a-c) — (a+b-2c)(a-b) при любых значениях a,b,c равно 0
С доказательством справится школьник, а вот кто придумал и как??? саму формулу, превращающую любые 3 числа в 0 — вот вопрос?
 Ответить
Ответить
Ответ для Александр Зикеев
a+b+c — a-b-c =0
(a-b) +(b-c)+(c-a)=0
а выражение
(b+c-2a)(c-b) + (c+a-2b)(a-c) — (a+b-2c)(a-b)
вероятно, использовалось, для решения какой-то более сложной задачи, где уже работали квадраты чисел
 Ответить
Ответить
Ответ для Мария Голубева
Х2=25
Х=5
далее дискриминант
Д=4-(4*-15)=64
х1=3. х2=-5
 Ответить
Ответить
Ответ для Мария Голубева
в примере идет сложение (x+5)*(x-3)+(x-5)*(x+5)
x2-3x+5x-15+x2+5x-5x-25
Далее складываем подобные
2x2+2x-40=0
дискриминант
x1=-5
x2=4
 Ответить
Ответить
 Ответить
Ответить
Ответ для ???????? ???????
Такое устроет?
 Ответить
Ответить
2(3а-4)-8а=
10-(-5(а-3)+а=
а-(b-(a+b))=
a=0, b=-1, тогда 2а-3b=
a=0, b=-1, тогда3 а+2b=
x=5, у=1, тогда 1,2-7у=
а=2,b=5, тогда 4а-1,8b=
7x-((y-x)+3y)=
5c-(2c-((b-c)-2b))=
Срочно нужно.
 Ответить
Ответить
Ответ для Наталья Сухарева-Штонденко
10-(-5а+15)+а=10+5а-15+а=6а-5;
а-(в-а-в)=а-в+а+в=2а:
2 · 0-3 · (-1)=3
3 · 0+2 · (-1)=-2
1.2 · 5-7 · 1=6-7=-1
4 · 2-1.8 · 5=8-9=-1
 Ответить
Ответить
 Ответить
Ответить
x8+x4+1
x4+x2y2+y4
a3+3a+2
x3+3x2-4
 Ответить
Ответить
Ответ для Сергей Аколоцев
(x2 + xy + y2)(x2 — xy + y2)
 Ответить
Ответить
Ответ для Алина Грегарищенко
 Ответить
Ответить
Ответ для Катюша Кретова
418z-532=203
418z=735
z=1,758373205741627
 Ответить
Ответить
Алгебра 7 клас Мерзляк, Полонський, Якір
Видавництво: Гімназія
 Ответить
Ответить
Ответ для Аня Лагутіна
 Ответить
Ответить
Ответ для Нурай Бишеева
| 1 |
| 5ab-6 |
| b6 |
| 5a |
| 125a3 |
| b18 |
 Ответить
Ответить
 Ответить
Ответить
Ответ для Лиза Миллер
S = 3 · (80 + 60) = 3 · 140 = 420
Ответ : 420
 Ответить
Ответить
владеют английским языком.Каждый из этиж людей обладают двумя из перечисленных навыков.Сколько всего человек в классе? Сколько человек говорят на английском и умеют программировать?
 Ответить
Ответить
Ответ для Олег Грицук
 Ответить
Ответить
 Ответить
Ответить
Ответ для Людочка Нища
42: 7 = 6 кнопок на каждом плаще.
6 · 11 = 66 всего кнопок для 11 плащей.
Ответ: 66 кнопок.
 Ответить
Ответить
Ответ для Александра Карась
 Ответить
Ответить
 Ответить
Ответить
Ответ для Аня Романовская
54 ?37 = 17
На сколько метров отрезали больше:
37 ?17 =20
Ответ: на 20 метров отрезали больше лески, чем осталось.
 Ответить
Ответить
Ответ для Марина Сапогова
37=7z-54
37+54=7z
91=7z
z=91:7
z=13
 Ответить
Ответить
| a2+ab |
| a2-b2 |
| ab(a+b) |
| a3-b3 |
| a2+ab+b2 |
| a3b + 3a2b2+3ab3+b4 |
 Ответить
Ответить
Ответ для Медет Андасбаев
| a2+ab |
| a2-b2 |
| ab(a+b) |
| a3-b3 |
| a(a+b) |
| (a-b)(a+b) |
| ab(a+b) |
| (a-b)(a2+ab+b2) |
| a(a+b) |
| (a-b)(a+b) |
| (a-b)(a2+ab+b2) |
| ab(a+b) |
| a2+ab+b2 |
| b(a+b) |
2)
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| a3b + 3a2b2+3ab3+b4 |
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| (a3b+b4)+(3a2b2+3ab3) |
=
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| b(a3+b3)+3ab2(a+b) |
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| b(a+b)(a2-ab+b2)+3ab2(a+b) |
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| (a+b)(b(a2-ab+b2)+3ab2) |
=
| a2+ab+b2 |
| a2+ab+b2 |
| (a+b)(a2b-ab2+b3+3ab2) |
| a2+ab+b2 |
| a2+ab+b2 |
| (a+b)(a2b+2ab2+b3) |
=
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| (a+b)b(a2+2ab+b2) |
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| (a+b)b(a+b)3 |
| a2+ab+b2 |
| b(a+b) |
| a2+ab+b2 |
| b(a+b)3 |
| a2+ab+b2 |
| b(a+b) |
| b(a+b)3 |
| a2+ab+b2 |
(a+b)2=(a+b)2.
Ответ: равенство верно.
 Ответить
Ответить
Ответ для Mohina Kurbanova
| 2 |
| 3 |
| 69 |
| 10 |
| 3 |
| 2 |
| 48 |
| 10 |
| 5 |
| 8 |
| 25 |
| 10 |
| 2 · 69 |
| 13 · 10 |
| 2 · 3 |
| 3 · 2 |
| 48 · 5 |
| 10 · 8 |
| 48 · 25 |
| 10 · 10 |
| 13 |
| 5 |
| 6 |
| 2 |
| 4 |
| 10 |
 Ответить
Ответить
(x +y)^2 ?(x-y)^2 при x=0,5.y=-0,5
(a +0,5b)^2-(0,5a +b)^2 при а=3, у=-2
(0,75х-0,25у)^2-(9,25х+0,75у)^2 при х=16, у=-16
^2 это значитв квадрате скобка
 Ответить
Ответить
Ответ для Екатерина Павлова
1) (-2+2)2+(-2-2)2=0+(-4)2=16
2) (0,5-0,5)2-(0,5-(-0,5))2=0-(1)2=-1
3) (3+0,5 ·(-2))2-(0,5 · 3 + (-2))2=22-(-,05)2=4-0,25=3,75
4) ((0,75 · 16 ?0,25 · (-16))2 ? (9,25 · 16 +0,75 · (-16))2= (12+4)2-(148-12)2=162-1362=256-18496=-18240
 Ответить
Ответить
54+37
42+49
83-35
56+28
2)В каждом выроажений измени одно число так, чтобы
действие выполнялось без перехода через разряд.Выполни действия.
 Ответить
Ответить
Ответ для Надя Софронова
2) Чтобы действие выполнялось без перехода через разряд, необходимо, чтобы результат действия для разряда давал результат 0<x<10. Т.е.
75-24
54+35
42+47
83-32
56+23
 Ответить
Ответить