На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Решение уравнений с пропорцией
Поддержать сайтНекоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.
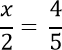
Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции, то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.

Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.
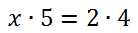
Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.
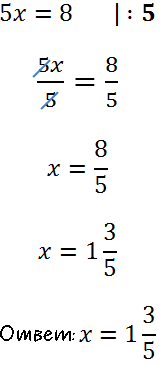
Рассмотрим другой пример уравнения с пропорцией.
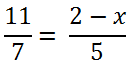
Такое уравнение также решается с помощью правила пропорции.

Если в члене пропорции присутствуют знаки «+» или «−», обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.
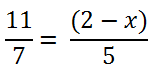
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции для дальнейшего решения.
Теперь раскроем скобки с помощью правила раскрытия скобок.
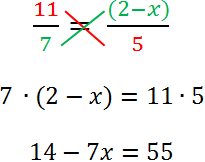
Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать правило знаков.
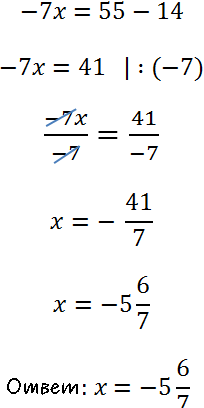
Иногда уравнения с пропорцией могут быть представлены следующим образом:
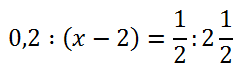
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение, в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
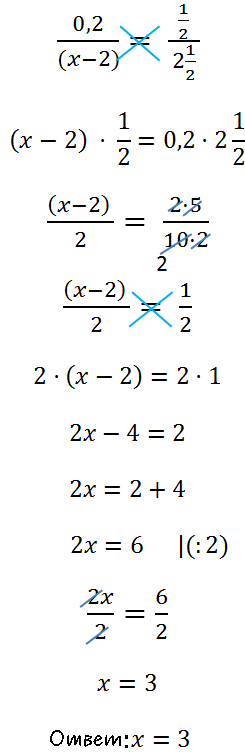
Другие примеры решения уравнений с пропорцией
-
=x 6 3x 18
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=3x 1,7 0,21 6,8
3x · 6,8 = 0,21 · 1,7
20,4 x=
·21 100 17 10
20
x =4 10 21 · 17 100 · 10
=204 · x 10 21 · 17 100 · 10
204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =21 · 17 · 10 204 · 1000
x =21 · 17 204 · 100
x =7 · 17 68 · 100
x =119 : 17 6800 : 17
x =7 400
Ответ: x =7 400
Ваши комментарии
Оставить комментарий: