На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Решение линейных уравнений 7 класс
Поддержать сайтДля решения линейных уравнений используют два основных правила (свойства).
Свойство № 1
или
правило переноса
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
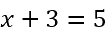
Вспомним, что у любого уравнения есть левая и правая часть.
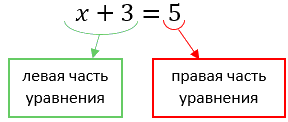
Перенесем число «3» из левой части уравнения в правую.
Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».
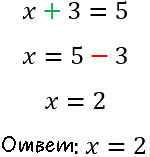
Полученное числовое значение «x = 2» называют корнем уравнения.

Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение.
По правилу переноса перенесем «4x» из правой части уравнения в левую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+».
5x = +4x + 9
5x − 4x = 9
Теперь приведем подобные и решим уравнение до конца.
x = 9
Ответ: x = 9
Свойство № 2
или
правило деления
В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
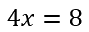
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
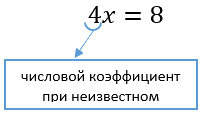
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».
Используем правило деления и разделим левую и правую части уравнения на «4». Не забудьте, что делить нужно и левую, и правую части.
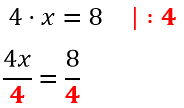
Используем сокращение дробей и решим линейное уравнение до конца.
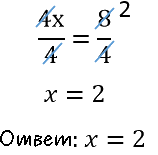
Как решить уравнение, если «x» отрицательное
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент. Как, например, в уравнении ниже.
Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить «−2», чтобы получить «1»?». Нужно разделить на «−2».
| −2x |
| −2 |
| 10 |
| −2 |
x = −5
Ответ: x = −5
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно применять оба свойства (правило переноса и правило деления).
Также требуется вспомнить правило раскрытия скобок и правило приведения подобных.
-
25x − 1 = 9
25x = 9 + 1
25x = 10 |: 25
=25x 25 10 25
x =2 5
Ответ: x =2 5
-
11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −6
11y − 44 + 50 − 30y − 12 + 9y = −6
11y − 30y + 9y − 44 + 50 − 12 = −6
20y − 30y + 6 − 12 = −6
−10y − 6 = −6
−10y = −6 + 6
−10y = 0 |:(−10)
=−10y −10 0 −10
y = 0
Ответ: y = 0
Ваши комментарии
Оставить комментарий:
 Ответить
Ответить
Ответ для Одинахон Иномова
√39-5 = 2x
x = ((√39)-5):2
x = (6.2449979984 — 5):2
x = 1.2449979984: 2
x = 0.62249899919
или по формуле Герона √(a2 + b) = a +
| b |
| 2 * a |
√39-2x = 5
√39-5 = 2x
x = ((√39)-5)/2
x = (√(36+3) — 5)/2
x = (√(62+3) — 5)/2
x = ((6 +
| 3 |
| 2 * 6 |
x = (6
| 1 |
| 4 |
x = 1
| 1 |
| 4 |
x =
| 5 |
| 4 * 2 |
x =
| 5 |
| 8 |
 Ответить
Ответить
 Ответить
Ответить
Ответ для Егор Семенов
| 4x |
| 3 |
| 3 |
| x |
 Ответить
Ответить
 Ответить
Ответить
Ответ для Даня Буйновский
Так как 0.6 · ?0.7 = ?0.42, а ?0.42 +0.42 =0
 Ответить
Ответить
(P.S) Мне нужно полностью всё решение. Заранее — спасибо.
1) 0,9x ? 0,6 (x ? 3) = 2 (0,2x ? 1,3)
2) ? 0,4 (3x ? 1) + 8 (0,8x ? 0,3) = 5 ? (3,8x + 4)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Спасибо! Решено!
 Ответить
Ответить
Ответ для Антон Ершов
0,1x=4,4
x=44
2) ?1,2 +0,4 +6,4x ?2,4 =5 ?3,8x ?4
9x =3
x=
| 1 |
| 3 |
 Ответить
Ответить
Ответ для Макс Простов
3x +y=7
y=7 ? 3x
2x ?3(7 ?3x)=1
2x ?21 +9x=1
11x=22
x=2
y=7 ?3 · 2 = 1
Проверка:
2 · 2 ?3 · 1=1
3 · 2 +1=7
Верно
Ответ: x=2, y=1.
 Ответить
Ответить
Ответ для Макс Простов
x1=
| 7+5 |
| 4 |
| 12 |
| 4 |
x2=
| 7-5 |
| 4 |
| 1 |
| 2 |
Проверка:
2 · 0,52 ? 7 · 0,5 + 3 = 0
0=0
2 · 32 ? 7 · 3 + 3 = 0
0=0
2) D=25 ?4 · 3 · (-2) = 25 + 24 = 49
x1=
| 1 |
| 3 |
x2=-2
проверка аналогично.
 Ответить
Ответить
Ответ для Киара Артуровна
4x2? 7 = 0
4x2=7
x2=
| 7 |
| 4 |
x=±?(
| 7 |
| 4 |
 Ответить
Ответить
Ответ для Дарья Баширова
4X=29,1X
33,1Х=0
Х=0
Проверка:
0+3 · 0 = 9,7 · 3 · 0
0=0
Ответ: Х=0
 Ответить
Ответить






















