На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Решение линейных неравенств
Поддержать сайтПрежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше |
строгий знак (число на границе не включается) |
| < | меньше |
строгий знак (число на границе не включается) |
| ≥ | больше или равно |
нестрогий знак (число на границе включается) |
| ≤ | меньше или равно |
нестрогий знак (число на границе включается) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой знак сравнения: «>», «<», «≤» или «≥».
Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
Так как в неравенстве «x − 6 < 8» неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство

Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x < 8 + 6
x < 14
Итак, мы получили ответ к неравенству «x < 14». Но что означает такой ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу «x < 14» все решения неравенства, то есть область слева от числа «14».

Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство «x − 6 < 8» даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его вместо «x» в исходное неравенство «x − 6 < 8».

6 < 8 (верно)
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.

Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x < 14» можно понимать так: любое число из заштрихованной области (то есть любое число меньшее «14») будет являться решением неравенства «x − 6 < 8».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x» стоял коэффициент «1». Для этого достаточно разделить и левую, и правую часть на число «2».
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2». Так как «2» — положительное число, знак неравенства останется прежним.
2x (:2) > 16 (:2)
x > 8
 Ответ: x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
Используем правило переноса.
−3x ≥ −9
Разделим неравенство на «−3». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
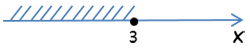 Ответ: x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
-
4(x − 1) ≥ 5 + x
4x − 4 ≥ 5 + x
4x − x ≥ 5 + 4
3x ≥ 9 | (:3)
3x (:3) ≥ 9 (:3)
x ≥ 3
 Ответ: x ≥ 3
Ответ: x ≥ 3
-
x + 2 < 3(x + 2) − 4
x + 2 < 3x + 6 − 4
x − 3x < 6 − 4 − 2
−2x < 6 − 6
−2x < 0 | :(−2)
−2x : (−2) > 0 : (−2)
x > 0
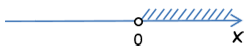 Ответ: x > 0
Ответ: x > 0
Ваши комментарии
Оставить комментарий:
Ответ для Алина Кирщина
Еще можно запомнить, как что где больше вершин у символа «птички», там большее число находится. У символа > слева две вершины, а справа одна, значит слева находится большее число.
 Ответить
Ответить
Ответ для Лина Недзвецкая
(3x − 5)/(x+1) > 0 ⇔ x < − 1 ∪ x > 5/3;
(3x − 5)/(x+1) ≤ 3 ⇔ 8/(x+1) ≥ 0 ⇔ x > − 1.
{(−∞; −1) ∪ (5/3; +∞)} ∩ (−1; +∞) = (5/3; +∞).
 Ответить
Ответить
Ответ для Sergey Gurzhiy
23 ? 6x<1
8 ? 6x<1
? 6x< ? 7
x>
| 7 |
| 6 |
 Ответить
Ответить
Ответ для Катя Петрова
Неравенство можно записать в виде
| (y — 8)(y — 2)2 |
| y — 9 |
Откуда y = 2 или 8 ? y < 9.
Стало быть, x = 1 или 3 ? x < log29.
 Ответить
Ответить
Ответ для Катя Петрова
 Форум задачиРешение:
Форум задачиРешение: Пусть y=2x , y>0
Пусть y=2x , y>0 Тогда y3 ? 3y2 +
Тогда y3 ? 3y2 +| 9y2 -288 |
| y-9 |
| 9y2-32y |
| y-9 |
-Tак как y>0, то сокращаем на y и преобразуем к виду


| y3-12y2+36y-32 |
| 9-y |
| (y-2)2(y-8) |
| y-9 |
Учитывая, что y=2x получим x=1 или (3?x<log29) Ответ: (x=1)?(3?x<log2). или так {1?[3;log29)}
 Ответить
Ответить
Ответ для Влада Навдушевич
| (x — 1)(x — 3) |
| x4(1 — x)(1 + x) |
и метод интервалов.
Ответ: (-oo; -1) U [3; +oo).
 Ответить
Ответить
Ответ для Надие Рахимова
x-4-3x>0
-4-2x>0
2x+4<0
2x<-4
x<-2
Проверка: Возьмём число меньшее -2, например -3
-3-4>-3 · 3
12>-9 Верно.
Ответ: x<-2
 Ответить
Ответить




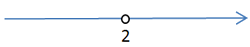 Это означает, что число
Это означает, что число  Это означает, что число
Это означает, что число 











