На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Как использовать разность квадратов a2 − b2
Поддержать сайтa2 − b2 Как применять квадрат суммы
(a + b)2 Как применять квадрат разности
(a − b)2 Как применять куб суммы
(a + b)3 Как применять куб разности
(a − b)3 Как применять сумму кубов
a3 + b3 Как применять разность кубов
a3 − b3
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.
Вспомним, как выглядит формула разности квадратов.
a2 − b2 = (a − b)(a + b)Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону.
(a − b)(a + b) = a2 − b2Как разложить на множители разность квадратов
Рассмотрим пример. Необходимо разложить на множители разность квадратов.
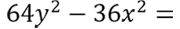
Обратим внимание, что «64y2» — это «(8y)2», значит, для формулы разности квадратов вместо «a» мы используем «8y».
Используем формулу разности квадратов. На месте «a2» у нас будет «64y2», а на месте «b2» стоит «36x2».
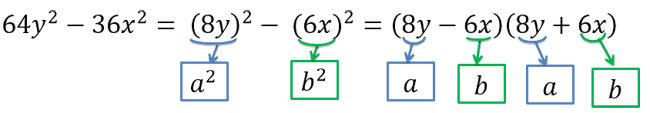
Разность квадратов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов обратно в разность квадратов, используя формулу сокращенного умножения.
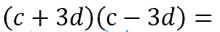
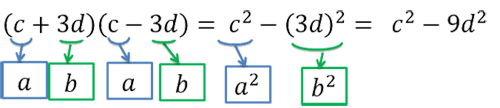
Обратим внимание, что произведение многочленов «(с + 3d)(с − 3d)» напоминает правую часть формулы разности квадратов «a2 − b2 = (a − b)(a + b)», только вместо «a» стоит «c», а на месте «b» стоит «3d».
Используем для «(с + 3d)(с − 3d)» формулу разности квадратов в обратную сторону.
Рассмотрим другой пример. Требуется упростить произведение многочленов.
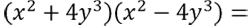
Если сравнить «(x2 + 4y3)(x2 − 4y3)» с правой частью
формулы разности квадратов
«a2 − b2 = (a − b)(a + b)», то
можно понять, что на месте «a» из первой скобки стоит «x2,
а на месте «b» стоит «4y3».

Одночлены, которые стоят на месте «a» или «b» как в формуле, могут стоять в степени.
Например, в рассматриваемом примере на месте «a» стоит «x2». Это означает, что именно «x2» мы рассматриваем как «a».
Используем формулу разности квадратов и решим пример до конца.
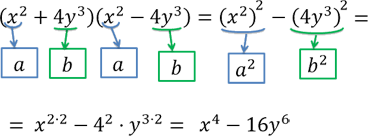
Рассмотрим пример сложнее. Требуется разложить на множители многочлен, используя формулу разности квадратов.
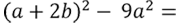
Представим «(a + 2b)2 − 9a2» как разность квадратов «a2 − b2».
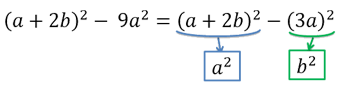

Одночлены, которые стоят на месте «a» или «b» как в формуле, могут быть в скобках, т.е. быть многочленами.
В рассматриваемом примере на месте «a2» стоит многочлен «(a + 2b)2». Это означает, что мы рассматриваем всю скобку «(a + 2b)» как «a» для формулы.
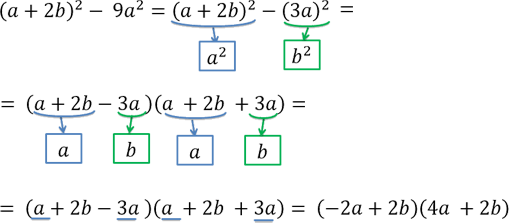
Решим пример до конца. После применения формулы разности квадратов не забудем привести подобные в примере.
a2 − b2 Как применять квадрат суммы
(a + b)2 Как применять квадрат разности
(a − b)2 Как применять куб суммы
(a + b)3 Как применять куб разности
(a − b)3 Как применять сумму кубов
a3 + b3 Как применять разность кубов
a3 − b3
Ваши комментарии
Оставить комментарий: