На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Как построить график функции вида «y = 7» или «x = 2 »
Поддержать сайт«y = kx + b» и её график Как построить график функции вида
«y = 7» или «x = 2»
Иногда в заданиях встречаются не совсем обычные функции, где в формуле функции есть только «y» или только «x».
Возникает вопрос: «Как построить график такой функции?».
Графиком функции вида «y = 7» и «x = 2» (функции, где есть только «y» или только «x») является прямая, которая параллельна одной из осей координат.
Как построить график функции «y = 7»
Разберемся на примере. Рассмотрим функцию «y = 7».
В формуле функции «y = 7» есть только «y». Это означает, что все точки графика функции «y = 7» имеют координату по оси «y» (ординату) равную «7».
Аргумент функции «x» явно отсутствует в формуле функции «y = 7», но тем не менее «x», пусть и «незримо», но есть в функции и принимает любые числовые значения.
С учетом выше сказанного давайте найдем несколько точек графика
функции «y = 7». Выберем три
произвольных числовых значения для «x». Например, числа «1»,
«2» и «3».
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 1 | 7 |
| (·)B | 2 | 7 |
| (·)C | 3 | 7 |
Отметим полученные точки на системе координат.
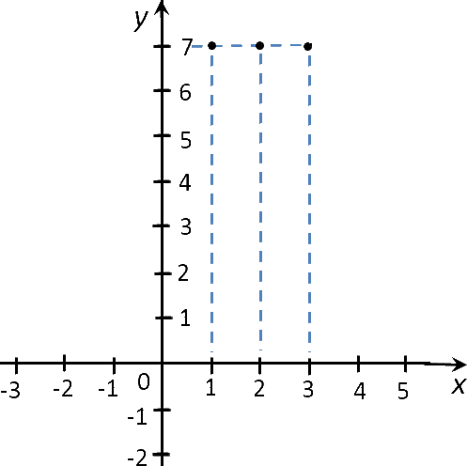
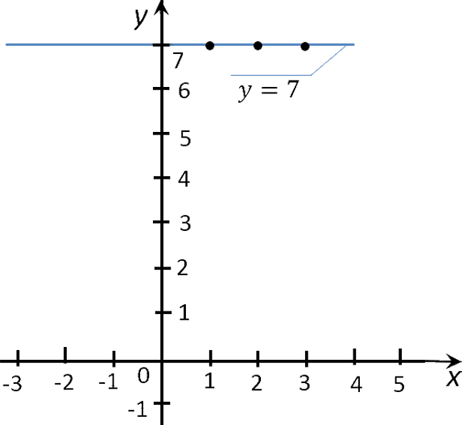
Если соединить полученные точки графика функции «y = 7», то мы получим прямую, которая параллельна оси «Ox».
Как построить график функции «x = 2»
Функции, где есть только «x» строятся по похожему принципу, что и функции, где есть только «y», с той лишь разницей, что теперь мы работаем с осью «Ox».
Разберемся на примере. Рассмотрим функцию «x = 2».
В формуле функции «x = 2» есть только «x».
Это означает, что все точки графика функции «x = 2» имеют координату по оси «x» (абсциссу) равную «2».
Значение функции «y» явно отсутствует в функции «x = 2», но тем не менее «y» «незримо» есть в функции и принимает любые числовые значения.
С учетом выше сказанного давайте найдем несколько точек графика
функции «x = 2».
Выберем три произвольных числовых значения для «y». Например, числа «1», «2» и «3».
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 2 | 1 |
| (·)B | 2 | 2 |
| (·)C | 2 | 3 |
Отметим полученные точки на системе координат.
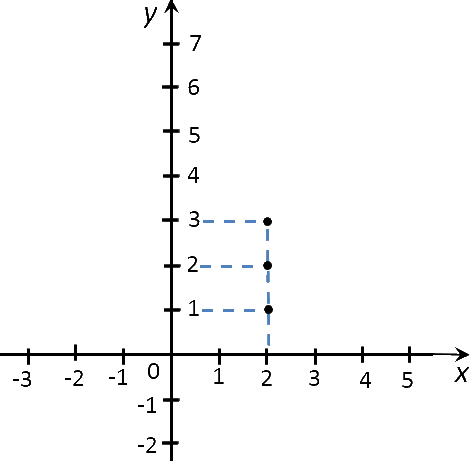
Если соединить полученные точки графика функции «x = 2», то мы получим прямую, которая параллельна оси «Oy».
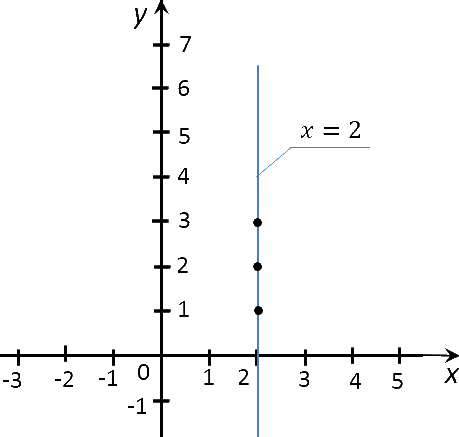
Как запомнить правила построения графиков функции вида «y = 7» и «x = 2»
Для построения графиков функции вида «y = 7» и «x = 2» следует запомнить следующее правило.
В функциях вида «y = 7» и «x = 2» график функции (прямая) «протыкает» ту ось, буква которой есть в формуле.
То есть, например, в функции «y = −3,5» есть буква «y». Это значит, что график функции «протыкает» ось «Oy» (ось ординат). Очевидно, что график функции «протыкает» ось «Oy» в точке «−3,5» на шкале оси «Oy».
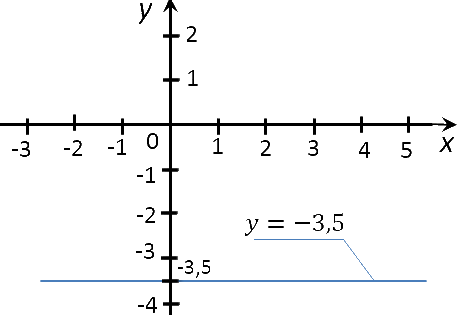
Теперь построим график функции «x = 1». В функции «x = 1» есть буква «x».
Это значит, что график функции «протыкает» ось «Ox» (ось абсцисс). Очевидно, что график функции «протыкает» ось «Ox» в точке «1» на шкале оси «Ox».
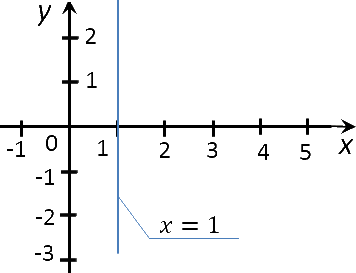
«y = kx + b» и её график Как построить график функции вида
«y = 7» или «x = 2»
Ваши комментарии
Оставить комментарий:






