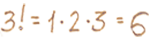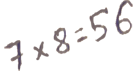На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Наименьшее общее кратное
Поддержать сайтДля того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу «a» — это число, которое само делится на число «a» без остатка.
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
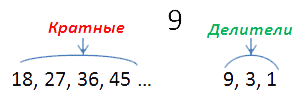
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
- Кратное числа «a»
обозначаем большой буквой «К».
К (a) = {…, …}
Пример. Найти НОК 6 и 8.
К (6) = {12, 18, 24, 30, …}К (8) = {8, 16, 24, 32, …}
НОК (6, 8) = 24
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
- Разложить данные числа на простые множители.
Подробнее правила разложения на
простые множители вы можете прочитать в теме
как найти наибольший общий делитель (НОД).
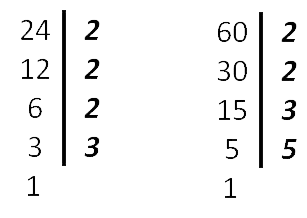
- Выписать в строчку множители, входящие в разложение
самого большого из чисел, а под ним —
разложение остальных чисел.
Запомните!60 = 2 · 2 · 3 · 5

Количество одинаковых множителей в разложениях чисел может быть разное.
24 = 2 · 2 · 2 · 3
- Подчеркнуть в разложении
меньшего числа (меньших чисел) множители,
которые не вошли в разложение бóльшего числа
(в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2 - Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).
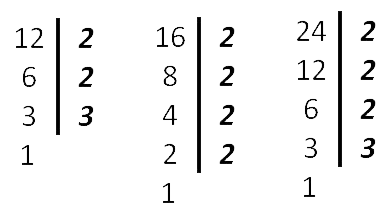 24 = 2 · 2 · 2 · 3
24 = 2 · 2 · 2 · 316 = 2 · 2 · 2 · 2
12 = 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16.
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
- Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60 - Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
кратное равно произведению этих чисел.
Пример.
НОК (8, 9) = 72

На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Ваши комментарии
Оставить комментарий:
Ответ для Елена Елена
НОК(360; 102) = 23 · 32 · 5 · 17 = …
 Ответить
Ответить
Я написала 1242, но 1242 при делении на 24 дает в ответе 51,75 будет ли это верным ответом?
 Ответить
Ответить
Ответ для Анвар Тынайбеков
Здесь есть решатель для примеров.
Убедительная просьба пользоваться поиском.
 Ответить
Ответить
 Ответить
Ответить
Ответ для Кирилл Журавлёв
А в супер-решателе можно себя проверить.
 Ответить
Ответить
 Ответить
Ответить
Ответ для Lera Kuchinskaya
 Ответить
Ответить
 Ответить
Ответить
Ответ для Андрей Алексеев
1) 4 — 24/4=6 — делитель 24. 4/2=2 — кратно 2.
2) 5 — 24/5=не делится без остатка — не делитель. 5/2 — не делится без остатка — не кратно 2.
И так далее.
Ответ: 4,6,12.
 Ответить
Ответить
Ответ для Евгений Мухамедшин
1) =
| 32+40-72 |
| 120 |
| 72-72 |
| 120 |
2) =
| 16+65-36 |
| 80 |
| 45 |
| 80 |
| 9 |
| 16 |
 Ответить
Ответить
 Ответить
Ответить