| 3 |
| 10 |
как сравнить это и пожалусто объясните



Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


 на главную
на главную
Также как и натуральные числа обыкновенные дроби можно сравнивать.
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.
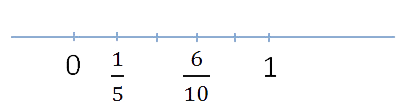
Равные дроби соответствует одной и той же точке на числовой оси.
На рисунке хорошо видно, что| 1 |
| 5 |
| 6 |
| 10 |
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
| 1 |
| 5 |
| 4 |
| 5 |
В обеих дробях одинаковый знаменатель равный 5.
В первой дроби числитель равен 1 и он меньше числителя второй дроби, который равен 4.
Поэтому первая дробь| 1 |
| 5 |
| 4 |
| 5 |
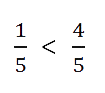
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
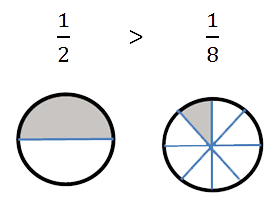
| 1 |
| 2 |
| 1 |
| 8 |
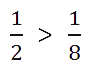
Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним| 2 |
| 7 |
| 1 |
| 14 |
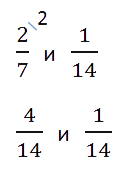
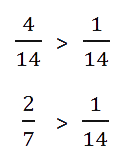
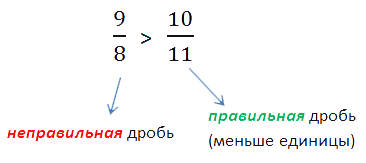
Это объясняется тем, что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Оставить комментарий:
| 21 |
| 10 |
 Ответить
Ответить
| 8 |
| 17 |
| 7 |
| 17 |
 Ответить
Ответить
 Ответить
Ответить
