| 1 |
| 12 |
| 5 |
| 6 |
| 3 |
| 4 |



Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


 на главную
на главную
При сложении дробей могут встретиться разные случаи.
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
Пример.
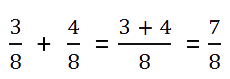
C помощью букв это правило сложения можно записать так:
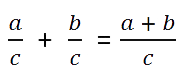
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.
Пример. Сложить дроби.
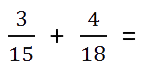
Находим НОК (15, 18).
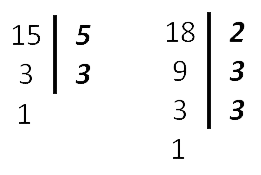 НОК (15, 18) = 3 · 2 · 3 · 5 = 90
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
| 3 |
| 15 |
| 4 |
| 18 |
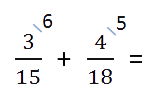
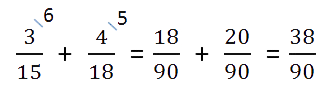
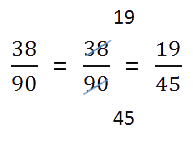
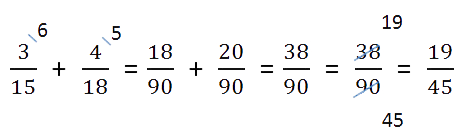
Сочетательное и переместитительное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
Пример.
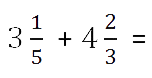
Складываем целые части.
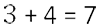
Если у дробных частей знаменатели разные, то сначала приводим их к общему знаменателю, а затем складываем.
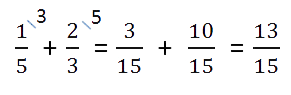
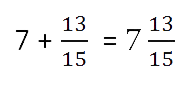
Ещё один пример на сложение смешанных чисел.
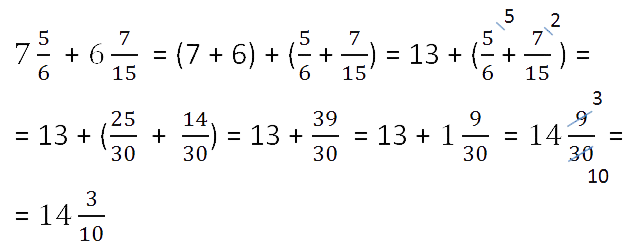
Оставить комментарий:
| 1 |
| 12 |
| 10 |
| 12 |
| 9 |
| 12 |
| 25 |
| 12 |
| 22 |
| 12 |
| 9 |
| 12 |
| 3 |
| 12 |
| 9 |
| 12 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 4 |
| 1 |
| 3 · 4 |
| 4 · 1 |
| 1 |
| 12 |
| 10 |
| 12 |
| 25 |
| 12 |
| 22 |
| 12 |
| 3 |
| 12 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 1 |
| 1 · 3 |
| 4 · 1 |
| 3 |
| 4 |
 Ответить
Ответить
| было очень непонятно |
| теперь понятно + + |
 Ответить
Ответить
| 3 |
| 7 |
| 90 |
| 7 |
| 5 |
| 6 |
| 70 |
| 6 |
| 90 |
| 7 |
| 70 |
| 6 |
| 540+490 |
| 42 |
| 1030 |
| 42 |
| 22 |
| 42 |
| 11 |
| 21 |
 Ответить
Ответить
 Ответить
Ответить
| 54 |
| 24 |
| 16 |
| 5 |
| 625 · 16 |
| 16 · 5 |
 Ответить
Ответить
 Ответить
Ответить
| 4 |
| 7 |
| 3 |
| 7 |
| 4 |
| 5 |
| 5 |
| 6 |
| 1 |
| 3 |
| 104 |
| 5 |
| 11 |
| 18 |
| 104 · 18 ? 11 · 5 |
| 198 |
| 1872-55 |
| 198 |
| 1817 |
| 198 |
| 35 |
| 198 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 29 |
| 3 |
| 2 |
| 5 |
| 29 · 5 + 2 · 3 |
| 15 |
| 151 |
| 15 |
| 1 |
| 15 |
 Ответить
Ответить
| 2 |
| 3 |
| 2 |
| 1 |
| 4 · 3+2 |
| 3 |
| 2 |
| 1 |
| 14 |
| 3 |
| 2 |
| 1 |
| 14+6 |
| 3 |
| 20 |
| 3 |
| 3 · 6+2 |
| 3 |
| 2 |
| 3 |
 Ответить
Ответить
| 2 |
| 3 |
| 2 |
| 1 |
| 14 |
| 3 |
| 2 |
| 1 |
| 14+2 |
| 3 |
| 16 |
| 3 |
| 5 |
| 3 |
 Ответить
Ответить