| 19 |
| 24 |
На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Периодическая дробь
Поддержать сайтНе все обыкновенные дроби можно представить в виде конечной десятичной дроби.
Например, если делить 2 на 3, то сначала получим ноль целых, потом шесть десятых, а затем при делении всё время будет повторяться остаток 2, а в частном — цифра 6.
Такое деление закончить без остатка невозможно и поэтому дробь| 2 |
| 3 |
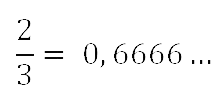
Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.
В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.
Вместо 0,666… пишут 0,(6) и читают «ноль целых и шесть в периоде».

Перевод периодической дроби в обыкновенную
Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь.
Рассмотрим периодическую дробь 10,0219(37)
- Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву «k». У нас «k = 2».
- Считаем количество цифр, стоящих после запятой, но до периода десятичной дроби. Обозначаем количество цифр за букву m. У нас «m = 4».
- Записываем все цифры после запятой (включая цифры из периода)
в виде натурального числа.
Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначаем полученное число буквой «a».
a = 021937 = 21 937 - Теперь записываем все цифры, стоящие
после запятой, но до периода, в виде натурального числа.
Если вначале до первой значащей цифры идут нули,
то отбрасываем их. Обозначаем полученное число буквой «b».
b = 0219 = 219 - Подставляем найденные значения в формулу, где «Y» — целая часть
бесконечной периодической дроби.
У нас «Y = 10».
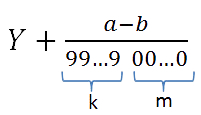
Итак, подставляем все найденные значения в формулу выше и получаем обыкновенную дробь. Полученный ответ всегда можно проверить на обычном калькуляторе.
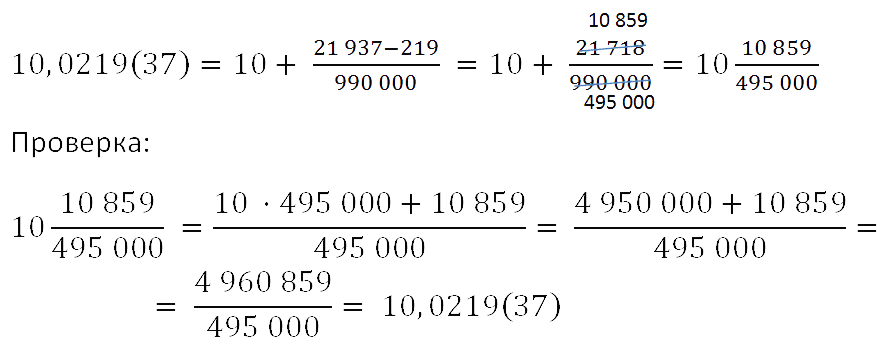
Ваши комментарии
Оставить комментарий:
Ответ для Артём Гусев
 Ответить
Ответить