Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!

Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
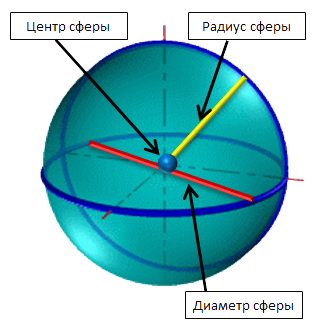
Важно!

Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!

Формула площади сферы:
S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)
Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:
S = 4 · πR2 =
4 · 3 ·
(1 ) 2 =
4 · ·
() 2 =
4 · ·
=
=
= =
=
=
45
м2
Как найти объем шара
Запомните!

- Формула объема шара:
V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
-
Вычислите радиус шара, если его объем равен
4 м3 (возьмите π как
3)
Выразим из формулы объема шара радиус.
Подставим в формулу известные нам значения. Число
π
возьмем как задано в задании «
3».
R3
= (3 ·
4) /
(4 · 3)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 ·
4 =
3 ·
=
=
Теперь снова подставим полученное значение в нашу формулу:
Важно!

Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2019 в 22:59
Руслан Магомедов
 Профиль
Благодарили: 0
Профиль
Благодарили: 0
Сообщений: 1
Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с
0
Спасибо Ответить
Ответить


 на главную
на главную