На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Арифметическая прогрессия
- Возрастание и убывание функции
- Геометрическая прогрессия
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Деление алгебраических дробей
Поддержать сайтПри делении алгебраических дробей пользуются правилами деления обыкновенных дробей.
Правила деления алгебраических дробей
Чтобы разделить алгебраические дроби нужно выполнить следующее:
- «перевернуть» дробь справа от знака деления « : »;
- заменить знак деления « : » на знак умножения « · ».
Рассмотрим пример деления алгебраических дробей.
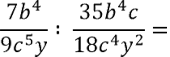
Перевернем алгебраическую дробь справа от « : » и заменим знак деления « : » на знак умножения « · ».
После этого умножим алгебраические дроби по правилам умножения алгебраических дробей.
При сокращении алгебраических дробей используем правила сокращения алгебраических дробей.

Рассмотрим другой пример. Требуется разделить алгебраические дроби, которые содержат многочлены и в числителе, и в знаменателе.
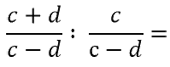

При делении алгебраических дробей, которые содержат многочлены и в числителе, и в знаменателе, заключайте многочлены в скобки целиком.
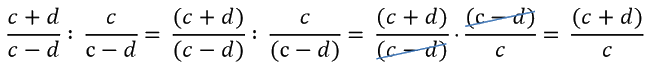
Как разделить алгебраическую дробь на одночлен (букву)
Рассмотрим пример деления алгебраической дроби на одночлен.
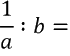
Представим одночлен «b» как алгебраическую дробь со знаменателем «1». Это можно сделать, так как при делении на «1» получается тот же самый одночлен.
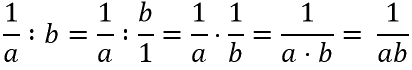
Рассмотрим пример деления отрицательной и положительной алгебраической дроби.
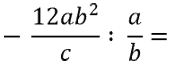
При делении алгебраических дробей не забывайте использовать правило знаков.
Перевернем алгебраическую дробь справа от знака деления « : ».
Заменим знак деления « : » на знак умножения « · ». Теперь определим итоговый знак по правилу знаков.
Первая алгебраическая дробь отрицательна, а вторая положительна. Правило знаков гласит: «Минус на плюс дает минус».
Значит итоговым знаком произведения будет знак «−».
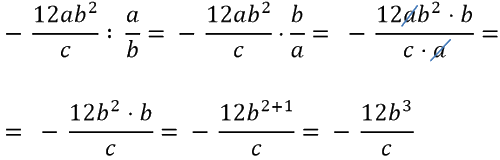
Ваши комментарии
Оставить комментарий:
Очень грамотно все расписано с объяснением.
 Ответить
Ответить







